オイラー法とルンゲ・クッタ法を使って微分方程式を解こう:無償ソフトで技術計算しよう【シミュレーション基礎編】(2)(1/2 ページ)
今回は、微分方程式を数値的に解く方法として、オイラー法とルンゲ・クッタ法について説明します。
筆者注:FreeMatはコマンド入力後にエンターキーを押すとコマンドを実行します。本連載ではエンターキーの記述を省略しますが、操作の際にはコマンド入力後にエンターキーが必要です。
今回は、微分方程式を数値的に解く方法として、オイラー法とルンゲ・クッタ法について説明します。
オイラー法
微分方程式の数値解法では、初期条件からわずかに値を増加させた点の値を計算し、さらに計算された点を元にわずかな値を増加させた点の値を計算します。その操作を繰り返します。
この際、オイラー法では微分の定義に基づいた(1)式を用います。
数値解法のプログラムでは、(1)式のf(x, y)の部分にsin(x)+yなどの具体的な式が入りますが、f(x, y)が複雑な式だと(1)式自体が複雑になります。そこで、「feval」コマンドを用いて、あらかじめ定義したf(x, y)を(1)式では呼び出して計算する方法を使ってみます。fevalコマンドはfeval(関数, 変数1,変数2)という形で用いて、関数に変数1と変数2を代入した値を返します。コマンドウィンドウ上で、試してみましょう。
--> f=inline('y/x')
f = inline function object f(x,y) = y/x
--> feval(f,2,1)
ans = 0.5000
inline('y/x')で、f=y/xという関数を定義します。すると、FreeMatはf(x,y)とアルファベット順に変数を並べて定義します。fevalでは、この順番で値を設定します。つまり、x=2、y=1だとすると、feval(f, 2, 1)とします。すると、fevalはy/xを計算して0.5と返します。
以上を用いて、FreeMatのプログラムにしたのが、ex401.mです。
clear;
f=inline('cos(x)');
x0=0;y0=0;xe=pi;n=11;
x=linspace(x0,xe,n);
y=zeros(1,n);
dx=(xe-x0)/(n-1);
y(1)=y0;
for k=2:n
y(k)=y(k-1)+feval(f,x(k-1))*dx;
end
yy=sin(x);
plot(x,yy,'o-',x,y,'*-');grid('on');
title(['Division Number= ',num2str(n-1)]);
xlabel('x');ylabel('y');
ここでは、例としてdy/dx=cos(x)を用います。sin(x)の微分はcos(x)となるので、dy/dx=cos(x)の初期値0での解析解は、y=sin(x)となります。ex401.mでは、dy/dx=cos(x)をオイラー法で数値的に解いた結果と解析解とをプロットして比較します。
f=inline('cos(x)')として、関数を定義し、x0、y0として初期値を与えます。計算の範囲はx0=0からxe=piまでです。n=11はlinspaceでの計算点数を指定します。分割数はn-1となります。計算効率を良くするためにy=zeros(1,n)でyの配列をあらかじめ用意しておきます。次に、分割幅dxを計算し、y(1)に初期値を入れます。後は、forループでk=2からnまで、y(k)=y(k−1)+feval(f,x(k-1))*dxを計算すれば、yの配列として解法結果が得られます。
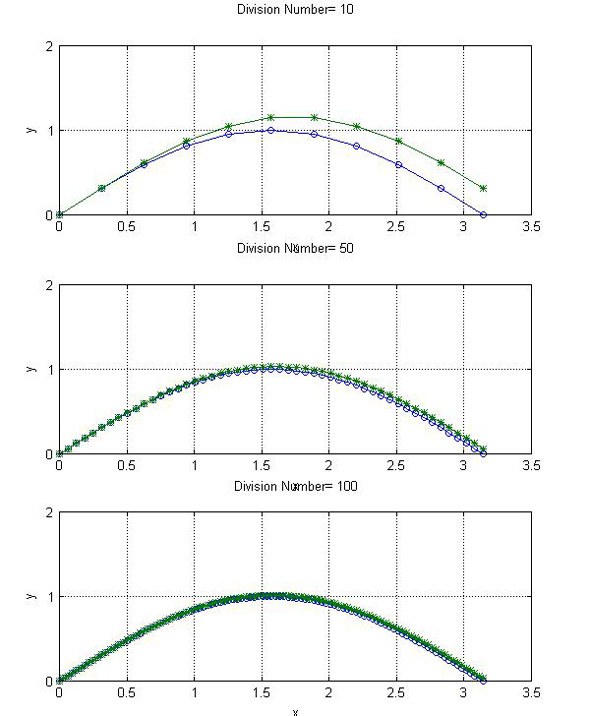
分割数を変えてex401.mで計算してみた結果が図1です。
図は横軸がxで、縦軸がyで、○が解析解、*が数値解を表します。上段の分割数10での結果は、数値解と解析解との差がxの増加に伴い広がっていることが分かります。中断の分割数50での結果では、この差は縮まっていますが、一致はしていません。下段の分割数100での結果では、数値解と解析解とがほぼ一致することが分かります。このように、オイラー法は、式が1つで分かりやすいという利点はあるものの、誤差が大きいという難点を抱えています。そのため、数値解法には、次に紹介するルンゲ・クッタ法が多く使われています。
Copyright © ITmedia, Inc. All Rights Reserved.