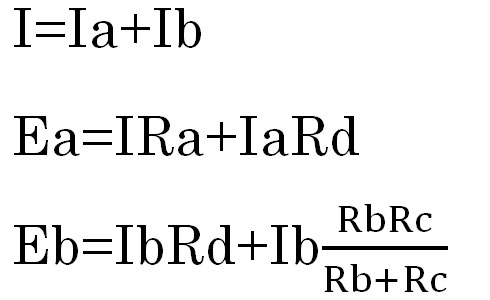抵抗とコンデンサ(その1)「キルヒホッフの法則」を知る:電子工作“超”入門(4)(2/2 ページ)
寒い日々が続いていますが、皆さんいかがでしょうか。東京でも小雪が舞うなど厳しい冷え込みの日々ですが、この前公園に行ったとき、桜に新芽が着いているのを見つけました。春は近いのかもしれません。
「キルヒホッフの法則」を知る
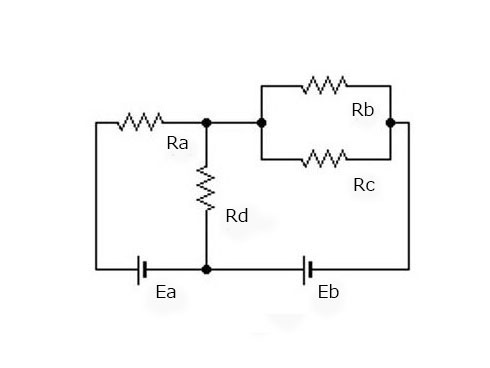
さて、実際の回路では回路図1〜回路図3のようなものはほとんど見かけません。下の回路図4のように、直列と並列それぞれが混ざり合って回路が構成されています。
こうした場合の抵抗値はどのように求めたらよいのでしょうか。ここで使うのが「キルヒホッフの法則」です。
キルヒホッフの法則
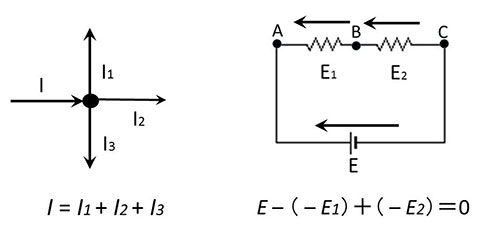
- 第1法則(電流則:KCL)
電気回路の任意の節点において、流れ込む向きを正(または負)と統一するとき、各線の電流Iの総和は0となる。
- 第2法則(電圧則;KVL)
電気回路に任意の閉路をとり電圧の向きを一方向に取ったとき、閉路に沿った各素子の電圧Viの総和は0である。
※ Wikipedia「キルヒホッフの法則 (電気回路)」より
ここで左側が第1法則、右側が第2法則です。電圧則のイメージが難しいと思いますが、電圧の向きを同一方向に取りますので、AB、BC間は抵抗により電位差が生まれ、それぞれマイナス方向の電圧となりますので、総和が0となるわけです。
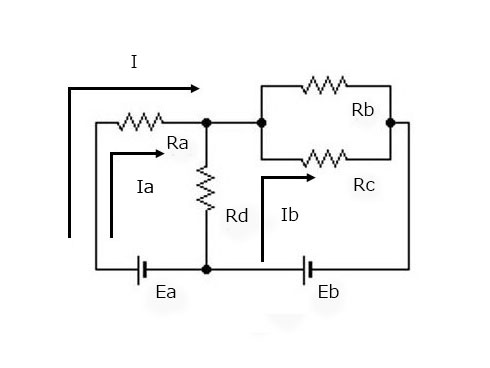
さてそれでは先ほどの回路図に戻ります。Eaを3V、Ebを1.5V、計算を簡単にするためRaからRdを1Ωと考えた場合の電流IaとIbの値を考えていきましょう。
キルヒホッフの法則から、左の海路に流れる電流はそれぞれ、I=Ia+Ibとなります。左側の回路を見たときには、以下の式が成立します。
これにそれぞれ3V、1.5V、1Ωの値を代入すると、Ia=2A、Ib=1Aとなります。回路図を見ていく際にはこうした知識があると、より理解が深まるでしょう。
次回はコンデンサとインピーダンスについて見ていくことにします。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 電子工作“超”入門(3):電子工作的な観点でコンデンサを知ろう
電子工作“超”入門(3):電子工作的な観点でコンデンサを知ろう
紅葉の季節も過ぎ、いよいよ本格的に冬へ入る季節になってきました。寒暖の差が激しい日が続いていますが、こういうときは体調管理が難しいですね。暖房器具を出そうか迷っていますが、とりあえずホットカーペットの電源を入れることにしました。 電子工作“超”入門(2):電子工作の基本のキ、抵抗を知ろう
電子工作“超”入門(2):電子工作の基本のキ、抵抗を知ろう
朝晩冷え込みを感じる昨今ですが、皆さんお元気にお過ごしですか?季節の変わり目は体調を崩すもの。かくいう私も少しカゼを引いてしまいました。でも秋葉原のパーツ屋さんに行くと元気になるのが不思議だったりします。 電子工作“超”入門(1):シンプルなポタアンを理解しながら作るための第1歩
電子工作“超”入門(1):シンプルなポタアンを理解しながら作るための第1歩
この連載は簡単なポータブルアンプの製作を通じて、抵抗やコンデンサの読み方といった、初歩的な電子回路についての知識を学び、電子回路に親しんでもらうのが目的です。今回は「電子回路の読み方」を見てみましょう。- 連載:アイデア・ハック!! Arduinoで遊ぼう
「こんなモノがあったらいいのに……」をArduino(アルドゥイーノ)で実現。電子工作初心者や回路の知識のない人だって大丈夫。筆者と一緒に、頭の中のアイデアをカタチにし、モノづくりの喜びや難しさを体験・体感してみよう! - 連載:Scratch 2.0で体験! お手軽フィジカルコンピューティング
電子回路が苦手な人のためのフィジカルコンピューティング入門。Webブラウザだけでプログラム開発から実行まで行える「Scratch 2.0」を用い、センサーの接続や外部デバイスのコントロールに挑戦する! フィジカルな世界とつながるプログラミングを体験することで、今までにない発想がひらめくかも!?