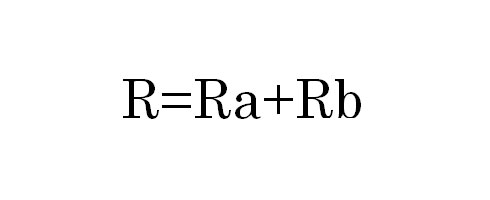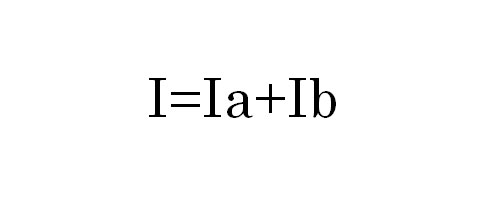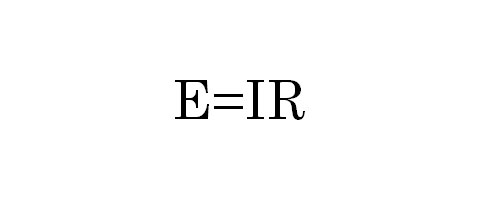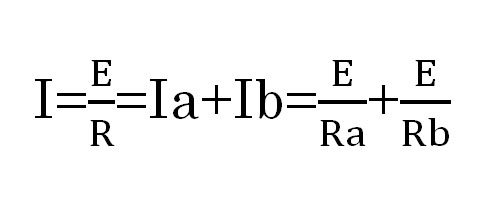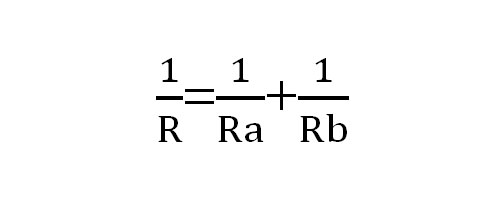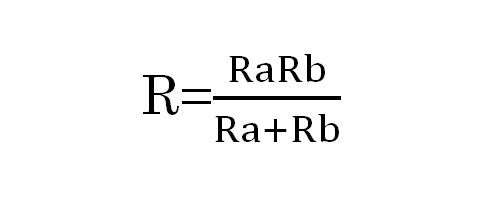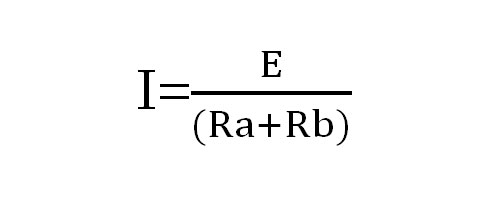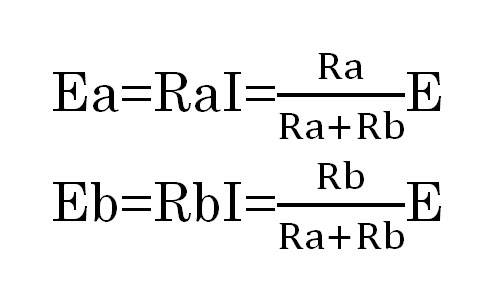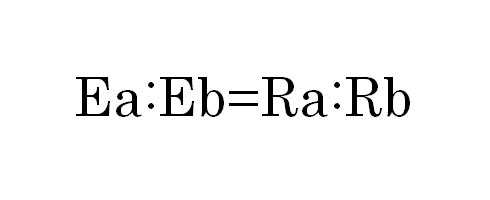抵抗とコンデンサ（その1）「キルヒホッフの法則」を知る：電子工作“超”入門（4）（1/2 ページ）

寒い日々が続いていますが、皆さんいかがでしょうか。東京でも小雪が舞うなど厳しい冷え込みの日々ですが、この前公園に行ったとき、桜に新芽が着いているのを見つけました。春は近いのかもしれません。

LINE

Hatena

　簡単なポータブルアンプの製作を目標として、抵抗やコンデンサの読み方といった初歩的な電子回路についての知識を学び、電子回路に親しんでもらう連載「電子工作“超”入門」。さて第4回の今回から数回にわたって取り上げるのは「抵抗とコンデンサ」です。

　ただ、「抵抗とコンデンサ」といっても内容は多岐に渡るため、今回は抵抗について見ていきます。回路図と計算式が多く出てくるのでスッと頭に入らないかもしれませんが、この理解が明日の勝利につながります。がんばっていきましょう。

抵抗の直列と並列のつなぎ方

　電子回路は抵抗やコンデンサ、トランジスタ、ICなど、さまざまな部品をつなぎ合わせることで成立しています。今回は抵抗とコンデンサについて、そのつなぎ方から組み合わせまで見ていきましょう。

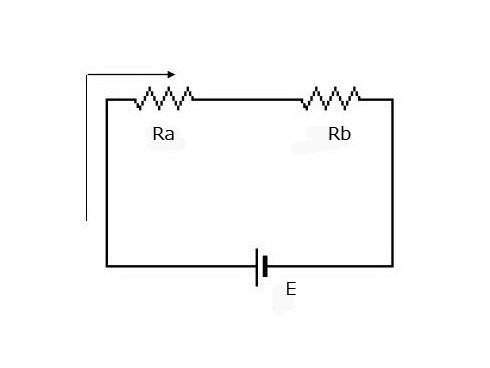
　まずは、2つ以上の抵抗がつながっている場合の抵抗値を求めます。

回路図1

　上のように2つの抵抗が直列接続している場合、RaとRbの合成抵抗Rの値は

で求められます。これは直感的に分かるので簡単ですね。

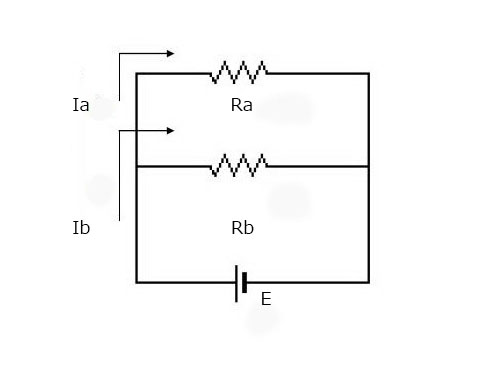
　今度は並列に接続している場合を考えてみましょう。

回路図2

　上記のように並列に接続している場合は、この回路に流れる電流Iから考えていきます。電源から流れる電流はRaとRbに分かれて流れていきますから、RaとRbに流れる電流IaとIbはそれぞれ、

　で表すことができます。

　この回路にかかる電圧Eとの関係を見てみます。同じようにその昔、電子回路を勉強したとき、電圧Eと電流I、抵抗Rの関係は

　で表せることを覚えていますでしょうか。これを「オームの法則」と言います。この公式をこの並列回路に適用します。この回路に流れる電流Iは

　これを電圧Eで割ると、

　抵抗Rから始まる式に直すと、

　これで合成抵抗Rが求まりました。なお、上記のように複数の抵抗を1つにまとめて電源と抵抗が1つずつ接続しているように見る回路のことを「等価回路」と言います。合成抵抗と等価回路については、その用語を覚えておきましょう。

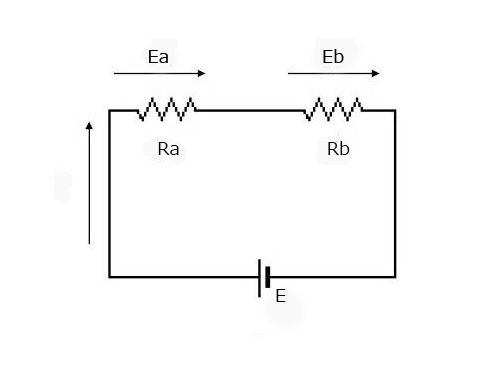
　今度は以下のような回路を考えてみましょう。

回路図3

　この場合、回路に流れる電流値Iは

　ですので、それぞれの抵抗にかかっている電圧は次のようになります。

　このように考えることを「分圧」と言います。分圧と抵抗の比は

となり、両端の電圧の比はそれぞれの抵抗値の比によって表せることが分かります。