非線形の場合も、難しいことをしなくて大丈夫!:独学! 機械設計者のための自動制御入門(12)(2/3 ページ)
実現象の多くは非線形。でも、線形のボード線図を少し変えて、シミュレーションを併用すれば大丈夫!
バックラッシの伝達特性
そういうこっちゃ。このままじゃ、あかん。そこでバックラッシの特性は実験で求めることにしよう……。しかし、これは面倒や。そこでシミュレーションで仮想実験をして求めるんや。
なるほどね。シミュレーションならば、わざわざ歯車を作る必要もないからすぐできるね。
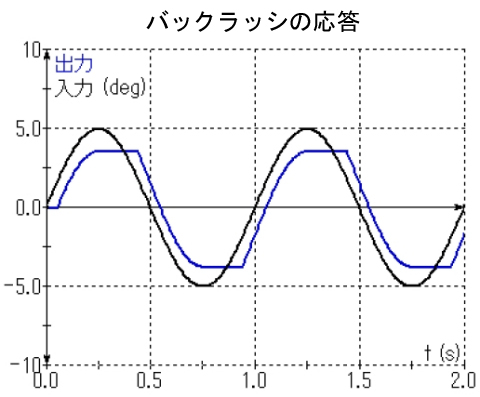
図5とアニメーション1はその結果だ。
バックラッシがあると出力が遅れるね。
そうなんや、バックラッシは出力を遅らすんや。遅れが発生するとどうなる?
フィードバックシステムは不安定になるね。
そう。バックラッシが大きいと遅れも大きくなるから、システムはより不安定になる。だからギアを何段も積み重ねたシステムは不安定になりやすいんや。
ギアを介さずに負荷を駆動する方法、つまりダイレクトドライブが好まれるのはバックラッシがない分遅れがなくなるからなんだね。
そういうこっちゃな。そして、バックラッシによる遅れの大きさは、周波数によらず一定値やけど振幅によって値が違う。
へ〜え。
振幅が大きいと相対的にバックラッシの影響が小さくなるからや。
線形要素に、ある周波数の正弦波を入力すると、異なる振幅と位相遅れのある正弦波が出力されます。非線形要素の場合は、正弦波ではなくゆがんだ波が出力されます。しかし、周期性は保持されています。ゆがんだ出力は、入力周波数を基準として、その整数倍の正弦波が多数合成されたものとなっています。これらの正弦波の振幅は、入力周波数に近くて低い周波数ほど大きく、高い周波数ほど小さくなっています。そこで、振幅の一番大きい、入力周波数と同じ周波数の正弦波(基本波)だけを取り出して、それを出力として扱うことで、伝達関数を記述することにします。これは記述関数と呼ばれており、具体的には出力波形をフーリエ展開したときの基本波を意味しています。記述関数を使って、近似的に非線形の伝達特性を線形の伝達関数に表現することが可能です。
ただし、記述関数を利用するためには、フーリエ展開という数学的な処理が必要となります。しかしアニメーション1のように、シミュレーションを利用することで、フーリエ展開の知識がなくても、おおよそのゲイン特性や位相特性を求めることができます。
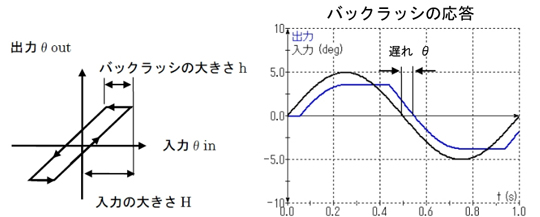
シミュレーションをすれば分かりますが、バックラッシの場合は、式(1)に示すように、周波数に関係なく遅れθが一定ですが、入力Hの大きさによって遅れθの大きさが変わります。
入力の大きさによって出力の遅れが違うんじゃ、どうやって制御設計をするのさ。
そこやねんな。皆、そこで苦労してる。でもな、逆転の発想でこの難問を解決できる場合もあんねん。
逆転の発想?
非線形を線形にすればいいねん。
どうやって非線形を線形にするのさ? そんなこと本当にできるの?
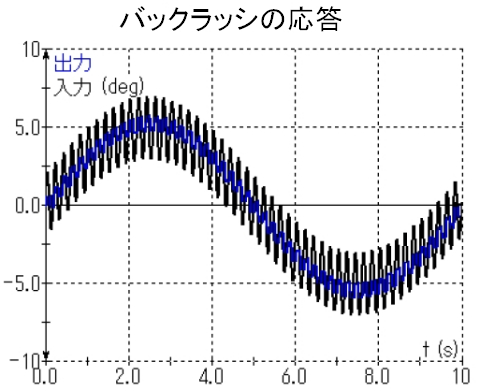
それができるんや。図7とアニメーション2は、その例だ。
何か、「出力がノイズだらけ」って感じだけど……。
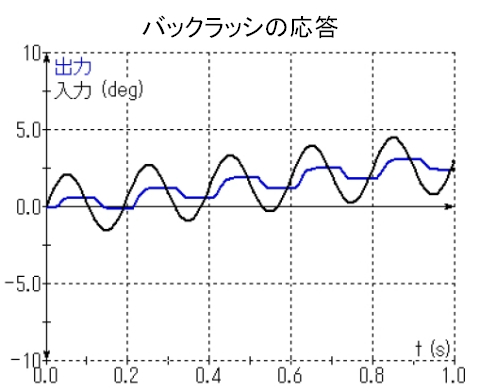
アニメーション2は、0.1Hzの5°の入力信号に5Hzの2°の正弦波を重ねたときの出力や。この5Hzの信号を「ディザ」って呼ぶんや。図8に示すように、ディザ(5Hz)に対しては出力は遅れるけど、本当に必要な0.1Hzの入力信号の出力には遅れがなくなってるのが、図7を見れば分かるやろ。
あれ? 本当だ。何でだろ?
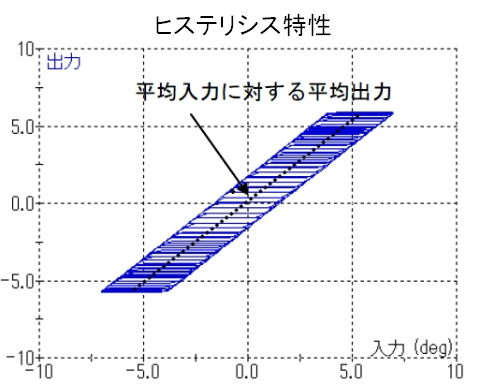
高周波小振幅信号(ディザ信号)の1つ1つに対しては遅れがあっても、図9のように、平均という視点でみれば平均入力に対する平均出力は線形と見なすことができるから、低周波信号に対しては遅れがなくなるんや。
でも、高周波信号(ディザ信号)が乗っている出力って、意味あるの?
例えば、ミサイルの操舵装置は、ミサイルが飛ぶ方向を制御するものやけど、操舵翼が高周波のディザ信号でぶるぶる震えていたって、機体制御には関係あらへん。
何で?
翼が小刻みにぶるぶる震えていても、機体はそれには応答せんからや。
あぁ、そうか。機体の周波数応答特性が、翼のぶるぶるに対してまったく反応しない。つまりその周波数域では、ゲイン特性はマイナス何十dBというレベルなんだね。
Copyright © ITmedia, Inc. All Rights Reserved.