非線形の場合も、難しいことをしなくて大丈夫！：独学！ 機械設計者のための自動制御入門（12）（3/3 ページ）

実現象の多くは非線形。でも、線形のボード線図を少し変えて、シミュレーションを併用すれば大丈夫！

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

むだ時間遅れとデジタル制御

　遅れ要素がフィードバックシステムを不安定にさせるということは、これまでたびたび説明してきました。従って、遅れが内在している非線形要素は制御設計にとって好ましいものではありません。しかし、現実の世界では、出力が入力に比例する要素のみで構成されていても遅れの発生する場合があります。例えば、プロセス制御では、一定時間の間隔で温度や圧力などの状態を計測します。そして、この計測値を基に、バルブ開閉の制御量を決めます。この時間遅れを「むだ時間遅れ」と呼んでいます。

　無駄時間Lの伝達関数は次式で表されます。

ですから、入出力の振幅比は1です。すなわち、

　　　ゲインは、0（dB）

　　　位相遅れは、arctan（Lω）

です。

むだ時間遅れは、プロセス制御特有のものでも何でもないで。昔のアナログ制御の時代はPIDコントローラーを電気回路で設計していた。だけど、いまはほとんどデジタル制御や。CPUとデジタル回路でPIDコントローラーを実現している。でも、デジタル制御だからこそむだ時間遅れが問題となることがあるんや。

どういうこと？

車の自動走行で言えば、車体の位置yをGPSで検知するとその値がCPUに読み込まれる。目標位置xとの偏差εをCPUが計算する。

まさしくコンピュータが得意な計算だね。

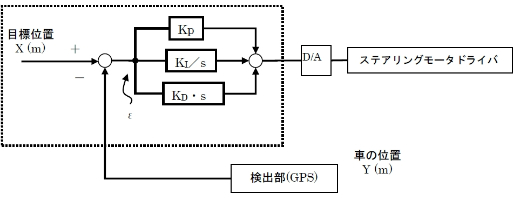
PID制御は、図10に示すように偏差εを比例（Proportional）、積分（Integral）、微分（Differential）したものの足し算だった。これらをCPUが演算し、ステアリングを駆動するモータドライバに出力する。つまり、CPUからD／Aコンバータを経て、モータドライバに電圧としてコマンドが行くんや。ただし、ドライバには常時コマンドが行っているわけではなく、サンプリングタイムと呼ばれる時間間隔ごとに命令が出される。

図10 自動運転制御コントローラーの構成

その時間間隔分だけ、制御すべき情報が遅れるわけだね。

そうや。理想は、車体の位置yをGPSで検知したと同時に、制御すべき制御量、この場合はモータドライバの電圧を出力したいんや。アナログ制御ではそれができた。しかし、デジタル制御ではその制御量を決めるためには比例（Proportional）、積分（Integral）、微分（Differential）の計算をしなければならない。この計算結果はサンプリングタイム間隔で出力される。だから、その分遅れるわけだ。

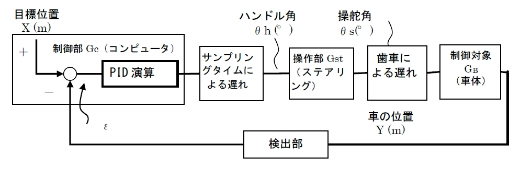
なるほど。複雑な計算をさせればさせるほど、サンプリングタイムを長く取る必要があるから遅れが大きくなるわけだね。するとデジタル制御でのブロック線図は、本当は図11なんだね。

図11 自動運転制御ブロック線

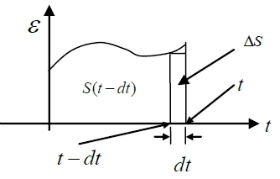
ところで、具体的にCPUにPID制御計算をどうやってやらせるの？ Pは比例といってるけど、要は掛け算のことだね。つまり、偏差εにある係数Kpを掛けるのはコンピュータが得意な計算だから分かる。偏差εをどうやって積分するの？ CPUの中にオペアンプが内蔵されているってことはないよね？

アナログ回路ではオペアンプが積分したり、微分したりしてくれる。つまりハードが瞬時に勝手にやってくれる。CPUで同じことをやろうと思えば、ソフトを使って演算しなければならない。まさしくコンピュータが得意とする数学の問題になるんや。この場合の積分は時間積分や。積分っちゅうのは、偏差εの時系列のグラフを描いたときに、時間軸とεの軌跡が囲んだ部分の面積や。図12から分かるように、時刻t-dtのときの面積S（t-dt）にdt時間経過したときの面積の増分ΔSを加えたものが、現在時刻tにおける面積S（t）だ。つまりdtをサンプリングタイムとすれば、

で計算できるっちゅうことや。

図12 積分

なるほど、dt時間前の面積（積分値）から現在の面積（積分値）を予測するんだね。じゃあ、微分は？

微分dε/dtの場合は積分の反対で、dt時間前のε（t-dt）と現在のε（t）を使って、

で計算できる。

これらにそれぞれの係数K_I，K_Dを掛けて足せば、PID制御が完成する。これをブロック線図に描いたのが図10なんだね。

そういうこっちゃ。これでおじさんが草太に教えたかったことは全て教えた。後は草太が実践によって自分のスキルをアップさせるだけや。

銀二叔父さん、いままでありがとう。これからも頑張るよ！

技術者にとって必要なこと

　現実の現象は複雑です。理論と呼ばれるものの多くは、それを簡単化して数式表現したものです。つまり、理論は絶対的に真というわけではなく、モデル化によって単純化したものが大部分です。すなわち多くが近似理論なのです。従って近似理論によって得られた解は実挙動を正確に再現したものではありません。しかし近似理論でも、上手に利用すれば、有益な知見を得ることができます。実際の挙動と、近似理論から得られた近似解とのすき間を埋めるのは、技術者としての知恵と経験なのです。

　技術者にとって必要なのは、理論に関する知識とそれを操る能力、そして経験に裏打ちされた知恵です。その両方を兼ね備えた者こそ、実力のある技術者だと思います。

　本連載が、これから自動制御を業務で実践しようと志しているエンジニアに、少しでも役に立つことができたならこれに勝る喜びはありません。読者の皆さん、長い間お付き合いくださり、どうもありがとうございました。

　　　　　　　　　　　　　　　　　　　　　――海風の吹く、明石の自宅にて。銀二

ご愛読ありがとうございました！

　今回で「独学！ 機械設計者のための自動制御入門」を終わります。

　最初は、自動制御理論を、なるべく数学を使わないようにと思いましたが、書き進めていくうちに、数式なしでは立ちいかなくなりました。しかし、よく見れば、どれも高校数学の域を超えていません。数学的な問題で本稿を読み進むことのできなかった人は、高校数学を復習した後、せひもう一度チャレンジしてみてください。

（終わり）

Profile

岩淵正幸（いわぶち まさゆき）

1953年生。技術士（機械部門）。日本セメント（現太平洋セメント）、川崎重工業精機事業部（現カワサキプレシジョンマシナリ）を経て、現在事務処理機器メーカーでシミュレーションを活用した設計方法の開発および設計コンサルティング業務を担当。川崎重工では、油圧制御システム設計、旧石油公団（現石油天然ガス・金属鉱物資源機構）委託研究による圧力波通信システムの開発研究、対戦車用ミサイル操舵装置の開発に従事。

*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***