連載
長さや形状、支点を変えて、四節リンクを自在変化!:メカメカリンクで設計しよう(3)(1/2 ページ)
クローズドループ構造の四節リンクは、リンクの長さ、形状、支点位置を変えることで、さまざまな動作が作れる。
前回は、クローズドループ構造の四節リンクで、揺動運動する機構において、対向するリンクが等長と不等長の場合の動作特性の違いを確認しました。今回は四節リンクの幾つかのリンクの長さや形を変えた場合の動作特性の違いや、固定する支点位置を変えて直角レイアウトにした場合の特徴を確認したいと思います。
【No.06】対向する可動リンクが等長で、その他が不等長の場合 1
駆動リンクと従動リンクが等長であり、中間リンクと固定リンクが不等長の場合を考えてみましょう。図1のアニメーションから、下記のことが分かります。
- 駆動リンクが反時計回り(CCW)し、中間リンクと従動リンクが一直線上に並んだときの角度αの位置で全てのリンクが拘束され、駆動リンクが最大回転位置となる。
- 駆動リンクが時計回り(CW)したとき、角度αまでは駆動リンクと従動リンクは反時計回転の時の動作と対称性を持って揺動をする。
- 駆動リンクが時計回り(CW)したとき、角度αを超えて中間リンクと従動リンクが一直線上に折り重なる角度βの位置で全てのリンクが拘束され、駆動リンクが最大回転位置となる。
- 駆動リンクが時計回り(CW)したとき、角度αから角度βまでの間、従動リンクはそれまでの動きに対して反転する。
【No.07】対向する可動リンクが等長で、その他が不等長の場合 2
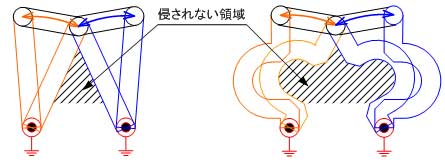
前述のNo.06のリンク機構において、駆動リンクと従動リンクの形状のみ変形させたものです。リンク機構を創造する場合、つい直線形状でリンク板を設計しがちですが、リンク板を自由形状とすることでさまざまなメリットが生まれます。図2のアニメーションから、No.06と同様の動作特性を持つことができます。
それでは、なぜリンク板を曲線で設計するメリットがあるのでしょうか? その答えを下記に示します。
【No.08】直角レイアウトで全てのリンクが等長の場合
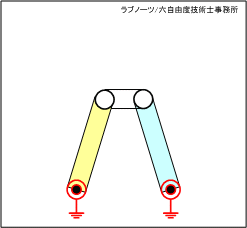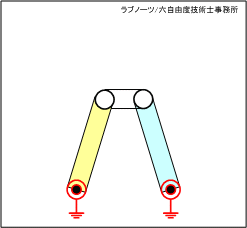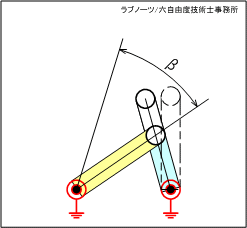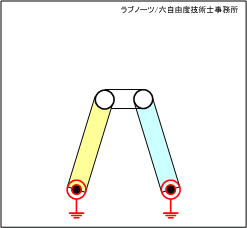
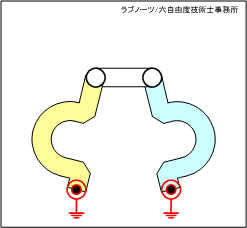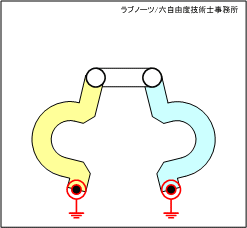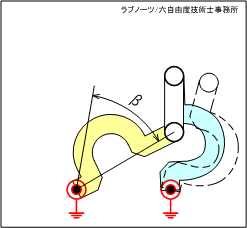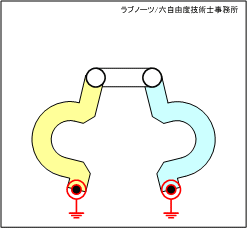
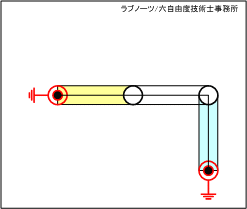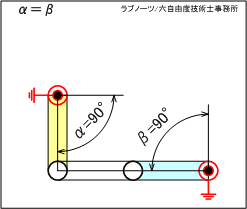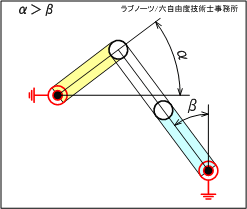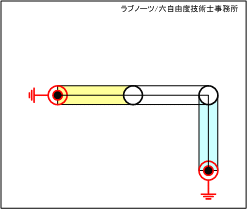
駆動リンクと従動リンク、中間リンク、固定リンクの全てが同じ長さで、支点位置を変更してリンクレイアウトが直角になる場合を考えてみましょう。図3のアニメーションから、下記のことが分かります。
- 駆動リンクを時計回転(CW)させると、最初は駆動リンクの動作角度αに対して従動リンクの動作角度βが小さい関係で動作する。
- その後、駆動リンクの動作角度α=90°(度)のときに従動リンクの動作角度β=90°になる。
- 上記の位置で中間リンクと従動リンクが一直線上に並ぶことで全てのリンクが拘束され、駆動リンクは最大回転位置となる。
- 駆動リンクを反時計回転(CCW)させると、常に駆動リンクの動作角度αが従動リンクの動作角度βより大きく動作する。
- その後、中間リンクと従動リンクが一直線上に並んだとき、全てのリンクが拘束され、駆動リンクが最大回転位置となる。
- 駆動リンクを反時計回転させた場合、時計回転させた場合の動作角度より小さい角度で最大回転角を迎える。
Copyright © ITmedia, Inc. All Rights Reserved.