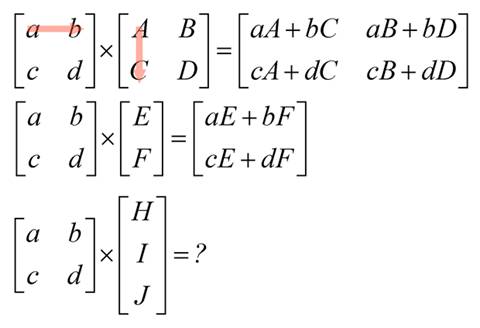まるでリーグ戦!? 剛性マトリクスを使って考える:設計者CAEを始める前にシッカリ学ぶ有限要素法(11)(1/2 ページ)
節点間のバネ定数が入ったマトリクスを作って総当たり戦! これが有限要素法解析の基本だ。
ブラック・ボックスの中身はこうだ!
本連載を通じて、フリーソフトで有限要素解析の実際についてたくさん説明してきました。皆さん、ご自身で体験されましたか? 体験できなかった方は、ぜひ、前回の「8分で検証! 手計算とフリーソフトの結果比較」(フリーソフト総集編)のムービーだけでもご覧になってください。
昔話は何の役にも立ちませんが、有限要素解析がフリーのソフトでできるなんて、20年前から考えると、まるで夢のようです。しかも、有限要素モデルがディスプレイに表示されるなんて……。昔はモデルをチェックするために、わざわざプロッタでメッシュ図を描きました。節点の座標値を1けた間違えて、プロッタが暴走。プロッタのロール紙1本使い切って、怒られるなんてこともありました。
さて、この連載もいよいよ終わりが近づいてきました。そろそろ有限要素解析の仕組みがどうなっているのか、具体的に説明したいと思います。
それではスタートです。
バネのカタマリをイメージしてみる
ここからの説明は、分かりやすくするために、数学的に、また材料力学的に不適切な表現になっているかもしれません。あくまでも有限要素法の仕組みをイメージしていただくためのものなので、そのあたりはどうぞ大目に見てくださいね。
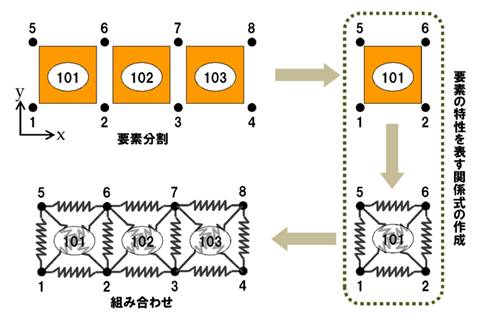
以前にも登場した、カンタンなモデルを例に、有限要素のプログラムは何をしているのか、説明してみます。
有限要素には、それぞれの要素の特性を表す数式があります。数式は複雑ですが、カンタンにいえば、要素の「硬さ」を表すと思ってください。要素は節点から構成されています。そして節点には6自由度があります。このあたりの話が分からない方は、ぜひこれまでの記事を読んでみてください。
本当は、3次元で表さなければならないのですが、今回は分かりやすくするために2次元で説明します。
要素の特性を表す数式によって、節点間に「硬さ」が定義されます。これを「剛性」といいます。これを模式的に「バネ」で表してみました。
本当は6自由度分のバネが必要ですが、今回はそれも省略して、モデルの平面、xy平面に作用するバネだけで考えます。こうなると有限要素モデルは、節点とバネのカタマリのようになります。僕の勝手なイメージですが、なんだか金属タワシみたいですね。
節点1を考えてみましょう。節点1は節点2と節点5、それに節点6とバネでつながっています。これは節点1が動こうと思った場合、節点1につながれたバネによって制約を受けます。その制約の強さは、バネの強さ、つまりバネ定数により決まってきます。
バネ定数といえば、そう「フックの法則」です。フックの法則は1本の式。有限要素モデルの節点同士のように、複雑なつながりを持った状況をフックの法則で表すにはどうすればいいのでしょうか……。
そこで登場するのがマトリクス(行列)です。
マトリクスの世界へようこそ
ここからちょっとだけ小難しい話になります。フックの法則はたった1本の式。節点と節点をつなぐバネのつながりをどう表現するのか。そこでマトリクスの考え方が必要になります。少しだけガマンして読んでみてくださいね。工学と数学が結びつく瞬間の美しい世界が少しだけ分かっていただけると思います。
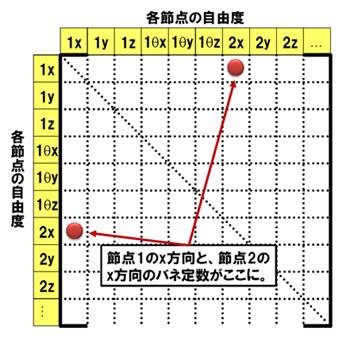
節点と節点の関係を整理するためには、総当たりのリーグ戦の表のようなものだと都合がいいですね。1つの節点で6自由度あるわけですから、節点1のx方向の自由度を1x、節点1のy方向の自由度を1y、というふうに、【節点番号+方向】という形式で、総当たり表のようなものを作ります。回転方向の自由度はθxのように表します。
今回の例題では節点は全部で8個ですから、6×8で48の項目が出そろうことになります。そして、そのリーグ戦の表の中をバネ定数で埋めていきます。本当はもっと難しいのですが、ここは極めて大ざっぱにバネ定数と考えてください。こうやって整理していくと、節点間のバネ定数が入った表が完成します。これを「剛性マトリクス」といいます。リーグ戦の表は、縦と横の数がチーム数と同じです。剛性マトリクスも縦と横、つまり行と列の数が同じです。図1の例の場合、48×48の行列ということになります。
有限要素法に詳しい方々や有限要素法のプログラムを作成するスキルがある方々には怒られそうですが、ここではイメージしていただくことを最優先としていますので、どうかご勘弁ください。詳しい内容をお知りになりたい場合は、ぜひ有限要素法の専門書をひも解いてみてください。
さて、この剛性マトリクス全体がフックの法則のバネ定数と考えてみましょう。……と、その前にマトリクスの演算について復習しておきます。行列については中学校と高校で習っているはずです。ぜひ思い出しながら読んでみてください。
図3の1番上の行列の掛け算を見てみましょう。2×2と2×2の行列を掛け算すると結果は2×2となります。
2番目の行列の掛け算は、2×2と2×1。結果は2×1となります。
それでは3番目の行列の掛け算はどうでしょうか。2×2と3×1。この行列の掛け算はできません。行と列の数が合わないからです。行列同士の掛け算は、掛けられる行列の列の数と掛ける行列の行の数が合っていなければならないからです。
Copyright © ITmedia, Inc. All Rights Reserved.