まるでリーグ戦!? 剛性マトリクスを使って考える：設計者CAEを始める前にシッカリ学ぶ有限要素法（11）（2/2 ページ）

節点間のバネ定数が入ったマトリクスを作って総当たり戦！ これが有限要素法解析の基本だ。

[栗崎 彰／キャドラボ，MONOist]

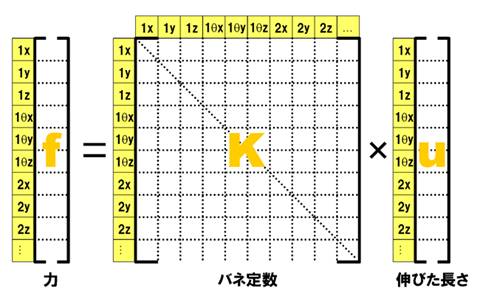
　さて、このことをアタマに入れて、フックの法則を行列で表現してみましょう。

図4 フックの法則を行列で表してみる

　ここで力に当たる「f」について見てみます。荷重とは有限要素法でどのように表されるでしょうか。前回、フリーソフトによる実習をしたように、有限要素モデルに掛ける荷重は、節点のある方向にある大きさの力を掛けることになります。方向と大きさ、つまりベクトルということになります。

　剛性マトリクスを構成した項目を思い出してみましょう。各項目は【節点番号＋方向】となっています。その項目に、大きさに当たる数字を入れれば、ベクトルとしての力を定義したことになります。前ページ 図1の例でいえば、48×1となります。

　同じように伸びた長さ「u」について見てみましょう。「伸びた長さ」とは有限要素法でいえば、変形量、つまり「求めるべき答え」ということになります。伸びた長さも力と同じように、節点が“ある方向に”“ある大きさだけ”動く、ということを意味します。変形量もベクトルということになります。これもベクトルですから、図1の例でいえば、48×1となります。“ある節点が”“ある方向に”動かないこと、つまり「変形量がゼロになる」こと、これが拘束です。

　図4で示した行列の掛け算は、行と列の数が合っているので、行列の計算式として成り立つことが分かります。

　剛性マトリクスは有限要素モデルから組み立てられるもの。そして、荷重は荷重条件として与えられるもの。そして拘束も拘束条件によって与えられるものです。

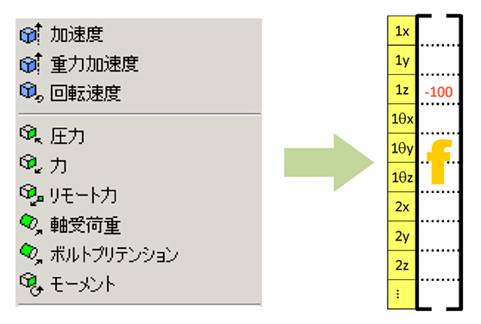
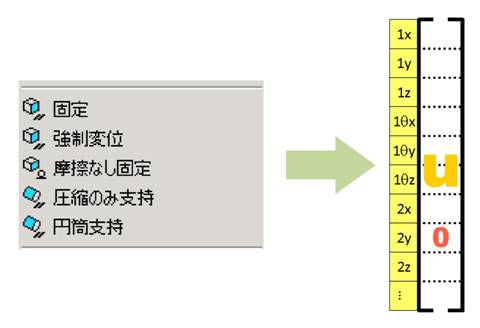
　荷重は48×1のマトリクスのある部分に数字が入ることになります。そして拘束条件は48×1のマトリクスのある部分をゼロにすることになります。

　ある設計者向けの解析ソフトウェアの荷重のアイコンを見てみましょう。何やら便利そうなアイコンが並んでいます。ここで理解しておきたいのは、どのアイコンを使っても、結局は節点に掛かるベクトルとして定義されることです。

図5 どんな荷重条件も結局はベクトルに置き換えられる

　それは拘束についても同じことです。それらしいアイコンが並んでいます。どのアイコンを使っても、結局は“ある節点の”“ある方向の”変形をゼロにするということになります。

図6 どんな拘束条件も結局は変形量がゼロに置き換えられる

　個人的な意見ですが、特に設計者が分かりやすい言葉に置き換えられている荷重や拘束の場合は要注意です。設計者に分かりやすい分だけ、それがどんな荷重や拘束を意味するのか調べないまま、使ってしまいがちだからです。

　本来であれば、荷重や拘束を定義するということは、荷重や拘束が“どの節点の”“どの自由度に”作用しているかを定義することです。つまり、設計者に分かりやすい言葉で表現された荷重や拘束が“どの自由度を“どうしているか”を理解している必要がある、ということです。

　自分が使おうとしている荷重や拘束のアイコンがどのように自由度に作用しているのか、小さいモデルでチェックしてから使うことを強くお勧めします。

そして変形量を求める

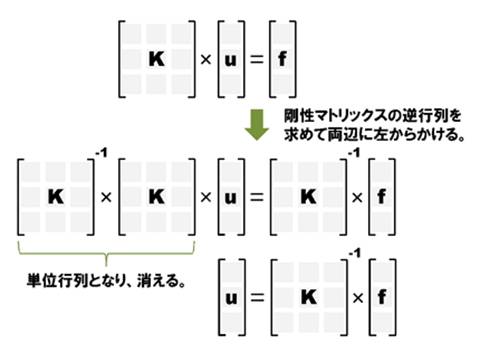
　ここまでくれば、あとは変形量を求めるだけ。「u」を計算します。フックの法則のように1本の式であれば、両辺を「k」で割るだけで、カンタンに「u」を求めることができますが、行列式となると、そうはいきません。

　行列式の割り算は、逆行列を求めて、それを左から掛けることによって成立します。懐かしい用語のオンパレードです。「逆行列」は「元の行列と掛けると、単位行列となる」行列。「単位行列」とは「対角項が1で、あとはすべてゼロで埋まった」行列のことです。

図7 剛性マトリクスの逆行列を求めて変形量を求める

　有限要素解析では、剛性マトリクスを組み立てるところと、剛性マトリクスの逆行列を求めるところにほとんどの時間が費やされます。

　長々と有限要素法の計算の仕組みのイメージを説明してきましたが、いかがでしたでしょうか。

　今回の内容でぜひ覚えておいていただきたいことは、以下のとおりです。

　これまでの連載で有限要素法の専門書を読むのに必要な基本中の基本だけは説明してきました。

　設計者のための解析については、まだまだ書き足りない部分があります。実物に即した拘束条件や荷重条件はどうすればいいか。静解析の適用範囲はどこまでか。周波数解析では何が分かるのか。……書きたいことはまだまだありますが、これらは実際の解析のテクニックの話で今回の座学の範囲外です。これらのテーマは別の機会に紹介することとして、次回でひとまず有限要素法の連載を終えたいと思います。

　次回は最終回として、有限要素法の座学についてまとめます。

Profile

栗崎 彰（くりさき あきら）

1958年生まれ。キャドラボ 取締役。1983年より24年間、構造解析に従事。I-DEASの開発元である旧 SDRC 日本支社、CATIAの開発元であるダッソー・システムズを経て現在に至る。多くの企業で3次元CADによる設計プロセス改革コンサルティングや、設計者解析の導入支援を行う。特に設計者のための講座「解析工房」が人気。解析における最適なメッシュ・サイズを決定するための「OK法」を共同研究で模索中。