ラプラス変換と複素数が導く！ ＋Dのご利益：独学！ 機械設計者のための自動制御入門（8）（3/4 ページ）

横風を受けて車がずれても元の位置に戻る仕組みはできた感じだけど、まだ何か足りない。PI制御の不足を補うのは？

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

応答性能はゲイン特性を見れば分かる

　銀二さんは、前回の復習を兼ねて、次のような説明をしました。

　線形システムでは、開ループシステムの伝達関数に振動数ωの正弦波xを入力したときの出力yは、振動数ωで、振幅がA倍、位相がθ進んだ正弦波です。つまり、

です。

　ここで、便宜上、入力を

と書くと、出力は、

となります。

　これを、複素指数関数表示すると、

となります。

　従って、伝達関数G₀は、

と表記することができます。すると、フィードバックシステムの伝達関数（閉ループの伝達関数）Gは、

ですから、閉ループGの振幅比｜G｜および位相∠Gはそれぞれ、

です。

　開ループGoのゲイン特性においてゲインが0（dB）のとき、すなわち入出力振幅比Aが1のときの周波数をωcとすると、一般に、周波数ωがωcを超えると振幅Aは小さくなりますから、ω＞ωcではA→0です。すると（11）、（12）から、

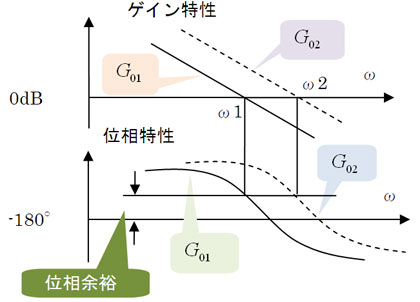
となり、ω＞ωcでは入力に追従できなくなります。従ってωcは閉ループシステムにおける応答性の目安ということになります。これをカットオフ周波数と呼ぶことがあります。ですから、図5の、では、カットオフ周波数ωcはそれぞれω1、ω2。ω2の方が高いので、の伝達特性を持つシステムの方が閉ループの応答性は高い、ということがいえます。

図5（再掲）

　ちなみに、開ループGoのカットオフ周波数では閉ループGの位相∠Gは、（12）から、

となり、開ループの伝達特性Goの位相遅れθが小さいほど、閉ループの伝達特性Gの位相遅れ∠Gも小さい、すなわち応答性が高いことが分かります。

通常、制御系の設計はシステムの安定性を重視するから、図5のG₀₁、G₀₂のように位相余裕は同じような大きさに設定する。だから、カットオフ周波数ωcが高ければ高いほど、応答性が高い、ということになるわけや

なるほど。すると、応答性を上げるためには開ループのボード線図のゲイン曲線を上に上げればいいってことだね

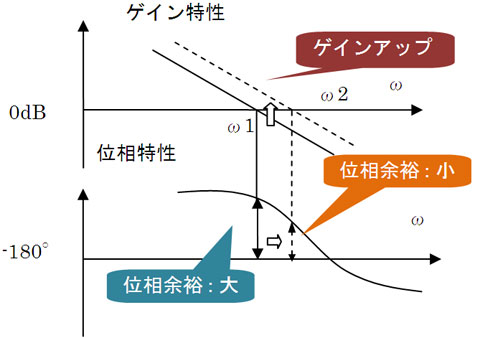
基本的にはそういうことなんやけど、ゲイン曲線を上げ過ぎると、図6で分かるように、位相余裕がなくなり不安定となる。せやから、むやみに上げることができないんや

図6 ゲイン曲線を上に揚げると不安定になる

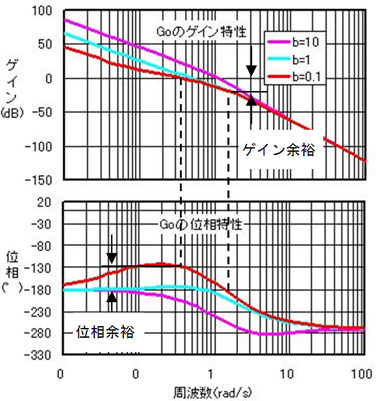
すると図4のボード線図から考えて、これ以上はゲインを上げることができないみたいだね

図4（再掲）

そこで、新たな補償方法が登場する……

比例、積分と出たから、ひょっとして今度は微分？

ご名答！

微分の周波数応答特性ってどんなんだろう？

自分で考えてみぃ