ラプラス変換と複素数が導く！ ＋Dのご利益：独学！ 機械設計者のための自動制御入門（8）（4/4 ページ）

横風を受けて車がずれても元の位置に戻る仕組みはできた感じだけど、まだ何か足りない。PI制御の不足を補うのは？

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

入力xが正弦波で

だから、その微分である出力yは

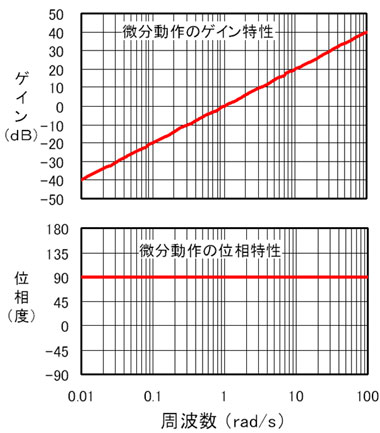
従って、ゲイン特性は、20log（ω）（dB）で、位相特性は周波数ωに関係なくπ/2、つまり90°進んでいるんだ。ボード線図に描けば図7のようになるね

図7 微分動作（補償）のボード線図

あるいは、入出力関係を微分方程式で表せば

これをラプラス変換すると

伝達関数をと書くことにすると

G_dif周波数応答特性を求めるためにはs＝i・ωと置いてやればよいから

従って伝達関数のゲイン特性は20log（ω）（dB）で、位相特性は周波数ωに関係なくπ/2、つまり90°進んでいる、ということが簡単に導ける

ラプラス変換や複素数表示に慣れると、物事がスムーズに進むね

そうなんや。数学の理論的厳密性にこだわらないで、数学をツールとして考えると、数学は非常に有用で便利なもんということが分かるやろ

そうだね……。それで、図7の微分補償を、コントローラのPI制御に加えると、伝達関数G1は、こういう形になるね

図7（再掲）

微分することを英語でいうと、『Differential calculus』やろ。だから微分による制御を微分動作と呼ぶんや。そして『Differential』のDを取ってD動作ともいう。PI制御に微分を加えた制御方法をPID制御と呼ぶんや。この制御方法は有名だから聞いたことあるやろ？

うん、うん、有名だね。とうとう、PID制御まで来たんだね。ところで、PID制御の効果については、またボード線図を使って説明するんだよね

そうや

実はさぁ、ボード線図の描き方についていま一理解していないんだよね。前回のPI制御の説明のときの図4のボード線図のときもあんまり理解していなかったんだ。それでさ、PID制御の説明を聞く前に、一度ボード線図の描き方を復習して整理しておきたいんだよね。そうしないと、PID制御の話を聞いても理解できないと思うんだ

図4（再掲）

そうやな。ボード線図をきちんと理解しておかないと、実務では制御特性を改善することができへんからな。それじゃあ、ボード線図の描き方を復習してから、今回解答できなかった草太の1つ目の疑問について考えてみよう。その後で、ボード線図を使ってどのようにPID補償をしていくか、その手順を説明しようか……

　周波数応答法では、ボード線図を使って補償制御を検討するため、ボード線図の描き方に慣れる必要があります。特に、PID制御の特徴を理解するためには、ボード線図についての理解が不可欠です。次回はあらためてボード線図の描き方について整理して説明します。

Profile

岩淵正幸（いわぶち まさゆき）

1953年生。技術士（機械部門）。日本セメント（現太平洋セメント）、川崎重工業精機事業部（現カワサキプレシジョンマシナリ）を経て、現在事務処理機器メーカーでシミュレーションを活用した設計方法の開発および設計コンサルティング業務を担当。川崎重工では、油圧制御システム設計、旧石油公団（現石油天然ガス・金属鉱物資源機構）委託研究による圧力波通信システムの開発研究、対戦車用ミサイル操舵装置の開発に従事。

*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***