赤い流れ星ジャアいわく「3σで統一したまえ」：公差解析 基本中の基本（6）（3/3 ページ）

量産製品のコスト削減を任されたけれど、品質が落ちないか心配。上手に部品を比較検討するヒントを例のおじさんが教える

[岡田あづみ／サイバネットシステム，MONOist]

坊や、コレは分散の加法性のルールを無視した計算の仕方ダYO！

もしかして、σのところ？

『ふふ、ラァラは賢いな』

ラァラ……

分散の加法性は、『寸法のつながりが線形表現できるアセンブリにおいて、その分散（σ2）の和はアセンブリの分散になる』んじゃな？（詳しくは第3回参照！）

思い出したわ！　デイちゃんとこの話したわね。だから分散にはそれぞれ同じ係数を掛けてあげないと、この関係は成立しないわね。リョウさん、私たちの関係も成立するように、愛の係数を掛けましょー

『ラァラ、ヤツとの戯言（ざれごと）は止めろ！』

何のことやら……今日は恋するオトメやらジャアもどきやら、騒がしいなぁ

そうか、分かりました！　いま僕が計算しているのは違うσのもの同士、すなわち違う次元の話だったんですね。僕としたことが！　大体考え方なんて誰からも教わったことなかったからな。いい勉強になります、おじさん

キャ！　何だかさわやかな反応だわ

ミーはジャアだってばYO！　しかし『ノビールスーツめ、やるようになった』ネ。この場合は概算だけど、比を使ってバラツキを統一〜！　3σで統一したまえ！

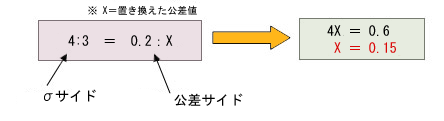
B社のバラツキは4σだったから〜……3σに直すとぉ……（図2）

図2　3σで統一したまえ

これって!!

0.6の4分の1は、0.15！　ふおぉーーー、A社もB社もσをそろえたら同じじゃないですかぁ!!

ふふ、これは数字のカラクリだネ。こりゃ危うくチャンスを逃すところだったね、坊や！

はい、これで何の迷いもなくB社に切り替える理由が見つかりました！　ありがとうございます、おじさん！　みんなもありがとう！

ノー！　ミーはジャア!! これからはσに気を付けて計算はするんだYO！　それでは、『勝利の栄光を君に！』、ジャアーッ

　おじさんは元気よく叫んで猛ダッシュで工場から消えていきました。

リョウさぁーん、無事、問題が1つ片付きましたね！　お祝いに今度2人で『千葉ネズミーランド』に行きたいなぁ、ココ

ハハハ……、そうだね。せっかくナオにも久しぶりに会えたし、今度の休みにでもみんなで行こうか！

帰りのJR総武線で

　ココは、リョウと2人きりでネズミーランドデートをしようとたくらみましたが、残念ながらはぐらかされ、OPT仲間で行くことになってしまいました。帰りのJR総武線車内では、機嫌を損ねたココがアズーとナオに始終八つ当たりです。

ちょっと、アンタたち！　一緒に連れて行ってあげるけど、気ィ効かせてリョウさんと私、2人きりにさせなさいよ！

ココ、ちょっと怖いー

うん。女子のすごさをあらためて知ったよ、今日は……

あら、そんなこというけれど、ナオの好きなAKP48だって女の子なんだから一緒じゃない！

ぬおー！　やめてくれっ！　オレの脳内ネズミーランドを汚さないでくれ！

ここまでのおさらい

　今回は「異なるバラツキで表された公差同士、どうやって積み上げるか？」、その方法を紹介しました。リョウのように購入部品を組み立てる場合や、工程内でも設計公差に対し異なるσ同士を組み立てる場合など、公差解析の場面において異なるバラツキ同士を積み上げるケースは割と多く見受けられます。このとき、σを無視して公差を積み上げてしまうと、出てきた結果は何σの結果なのか分からなくなってしまいます。もう一度分散の加法性の基本を理解し直すことで間違いのない計算を行いましょう！　（次回に続く）

Profile

岡田 あづみ（おかだ あづみ）

1978年生まれ。大学を卒業後、自動車部品メーカーに入社。生産技術の現場で公差解析に出会い、その後サイバネットシステム（株）に入社。現在は3次元公差マネジメントツール、「CETOL6σ」のアプリケーションエンジニアとして企業での公差解析の導入に携わる。