変化のない人生と伝達関数は、あり得ない？：独学！ 機械設計者のための自動制御入門（7）（2/4 ページ）

時間が十分経過したときの伝達関数の特性は、周波数応答特性で見れば低周波領域の特性に対応しているのはなぜ？

[岩淵 正幸／技術士（機械部門），MONOist]

でも周波数応答特性を求めるときの入力は正弦波だぜ。入力波形は複雑に変化すると思うんやけど、正弦波に限定するのはちょっと都合がよすぎないか

そんなことはないよ。複雑な入力波形も、異なる周波数の正弦波から合成されているから、それぞれの周波数に対する応答を重ね合わせれば、任意の入力に対する応答を予測することができるじゃん

重ね合わせが成立するシステムを線形システムというんだけど、実際のシステムは非線形だから、厳密にいえば、草太が説明したようにはならないんや。でも、近似的にはそう考えてもいい。いままでのところの説明で、草太がよく理解していることは分かった。システムの応答が入力周波数に依存することも理解してくれている。では話を元に戻して、制御対象の伝達関数Gsが∞となる入力周波数って、具体的にどうやって求めるんや？ そして、Gsが∞となる入出力状態とは、具体的にどういう状態や？

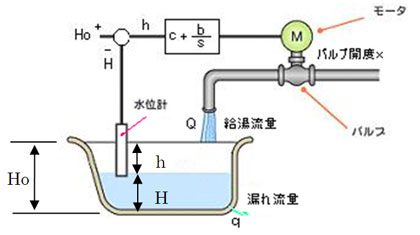
浴槽水位制御の場合、制御対象である浴槽については入力が給湯量Qで、出力が水位Hだったね。水位Hは給湯量Qを時間積分して浴槽断面積Sで割れば求まるから

入力Qを直接、正弦波で表現すれば、Hの周波数応答は、振幅をAとして

出力Hは、入力Qに対して、振幅が倍で、位相が90°（π/2）遅れた正弦波になる。（9-1）、（9-2）から、伝達関数Gs＝H／Qを求めると

これだと伝達関数は時間tによって変化することになる。しかし、システムが線形であると仮定すれば、入力が正弦波であれば出力も正弦波であることは分かっている。僕たちが知りたいのは、振幅比と位相遅れであって、波形の形状ではない。（10）には波形形状の情報まで含まれているためかえって使いにくくなっている。ところが、ラプラス変換と複素数のオイラーの公式を利用して伝達関数を表現すると、欲しい情報だけ抽出することができるんだ

（8）（9）は、ラプラス変換（ラブプラスじゃないからね？）を使って

ここでs＝iωとおくと、（10）はオイラーの公式を使えば

『伝達関数Gsによって、入力Qは、振幅が

倍で、位相が90°（π/2）遅れた正弦波の出力Hになる』……ということがカンタンに表現できる

よく勉強したな

まあね。分かり始めると興味がどんどん湧いてきて、自分で勉強するようになるのさ。それで叔父さんの質問の件だけど、Gsが∞となる入力周波数とは、（11）からω⇒0のときのことだよ

でも、図1の浴槽の水位制御では入力は、水位をHo＝60cmにせよ、という一定値入力であり、正弦波入力ではないぜ。それに入力周波数ω⇒0のときの応答って意味分からんし……

図（再掲）

叔父さん、前に教えてくれたよね。時間が十分経過したときの伝達関数の特性は、周波数応答特性で見れば低周波領域に対応しているって……だから、入力周波数ω⇒0のシステムの応答というのは、時間が十分経過したときのシステムの応答ということなんだ。つまり、ω⇒0はt⇒∞のときの応答を意味しているんだよ

ちょっとまった。確かに以前ワシはそういうたで。だけど時間が経過したとき、なぜ低周波での応答になるんや？ 叔父さんの受け売りではなく、草太のことばで説明してくれへんか？

そうなんだ。そこなんだ。そこが理解できれば制御系の静特性について、ほぼ理解したことになるんだけど……

どう解釈したら自分が満足できるか、学習のポイントはそこや。解釈はいろいろあろうけれど、叔父さんが『独学』で理解した、時間応答と周波数応答の関係について、叔父さんの解釈を説明させてもらうわ。草太は『非ユークリッド幾何学』って知っているか？

ユークリッド幾何学では平行線の存在を公理としているけれど、非ユークリッド幾何学では平行線も存在を認めていない。それでも幾何学としての体系が成立している、っていうヤツでしょ？

そうや。もし、非ユークリッド幾何学の側に立つならば、自然界には一定という状態は存在しないことになる

飛躍した理屈だね。なんで非ユークリッド幾何学を認めると、状態が一定というのが存在しないの？

x−y座標で、時間軸をx、状態をy軸にとって、一定状態であることを意味する直線をx軸に平行に引いてみぃ。平行線は存在しないんやから、一定状態を表す直線は必ず状態は必ずx軸と交わるってことやな。つまりこの世界は非ユークリッド空間だと思えば、伝達関数の入力も一定値ではありえない。無限時間後は必ず0となる。それは取りも直さず入力が周波数ω⇒0ってことやろ？ これは、人生についても同じことがいえる。変化のない人生はありえない。昔の人もいっている。『行く川の流れは絶えずして……』

『方丈記』はいいよ。とにかく、一見変化しないような状態も、実はゆっくり変化している。これを周波数で表現すればω⇒0に対する応答ということになるってことか……

実は、ラプラス変換の定理に最終値定理というのがあって、入力xが瞬間的に変化して、その後一定値を保つときの、t⇒∞のyの応答（ステップ応答）は、数学的にはω⇒0の応答に対応しているんや。つまり、無限時間経過したときの応答というのは、周波数ω＝0に対する応答に対応しているっちゅうわけやな。なぜならば、システムが発振しないことを前提とすれば、ω⇒0以外のすべての応答は消えてしまうからや

ということで、比例制御の場合Gcは一定値だから、（7）式を再掲する

外乱の影響

が残る。

外乱の影響をなくすためには、Gcが∞であればよいからω⇒0で∞となる積分制御をすればよい、ということになる。僕は、第5回で、比例制御では目標値に一致させることができないので、比例制御の代わりに積分制御をすることを思い付いた。あのときは直感的にそう思ったんだけど、こういう理論的な裏付けがあったんだね

しかし積分制御だけでは、ループを閉じたときシステムが発振してしまったんやな。発振メカニズムについては、第3回でも詳しく説明したけど、（6）からでも説明できるで。（6）から……

（14）のとき、出力yは∞となることは分かるやろ？ これをオイラーの公式を使って記述すると

つまり、開ループシステムの伝達関数G0が入出力の振幅比が1で、出力が入力より180°（π）遅れるようであれば、発振するっちゅうことや

*正確には以下である。「最終値定理とは、t⇒∞の応答yはラプラス変換ではL（y）⇒ｓ・G（s）・L（x）（s⇒0）である」。xがステップ入力の場合、L（x）＝1/sなのでt⇒∞では、L（y）⇒ｓ・G（s）/s＝G（s）（s⇒0）となり、s＝iωとおけばG（ω）（ω⇒0）である。

数学に慣れてくると、いろいろな物事がスパッと割り切れて見えてくるから不思議だね。浴槽水位制御の場合は、制御対象Gsが（11）で示される積分要素から構成されているから、出力は周波数に関係なく入力から90°遅れている。その上流の制御器Gcに積分をもってくると、さらに90°遅れて、開ループでは周波数に関係なく180°遅れることになる。一方、積分要素の振幅比は、低周波数では大きく、周波数が増加すると小さくなっていくから、振幅比が1となる周波数が必ず存在する。だから発振した

さっきは、周波数ω⇒0のときの応答について議論していたけど、今度は突然、振幅比が1で、位相遅れが180°となる周波数について議論している。話が飛躍してないか？

周波数ω⇒0は、t⇒∞の場合応答がどうなるかという議論。振幅比が1で、位相遅れが180°となる周波数はシステムが発振するかどうかという議論で、まったく別の話だよ。信号には必ずノイズが含まれているでしょ。ノイズは0から∞までの周波数成分を含んでいるから、システムが発振条件を満たせば、振幅は小さくても時間経過とともに発振するんだ。時間経過とともに振幅が大きくなっていく様子は第3回で叔父さんが説明してくれたとおりだよ

周波数ω⇒0は、発振しないことを前提として、t⇒∞の場合の応答がどうなるかという議論しているわけやな。それに対して発振するシステムでは、そもそもt⇒∞のときどうなるかなんて議論が意味あらへん。だから、話が飛躍したというより、前に戻って、安定性が保証されるかどうか確認しておこう、っちゅうことやな？

そういうことだね。……というわけで、制御器Gcは積分要素だけでは不十分だから、比例制御も加えたんだよね。これをラプラス変換表示で記述すると

s＝iωとおいて制御器Gcの周波数応答を見ると低周波数域の位相遅れは−90°だけど高周波数域では位相遅れが0°となっている。そのおかげで開ループシステムGoの振幅比が1のときの位相遅れを180°より小さくすることができたんだ。Goの振幅比1のときの遅れが180°より小さければ小さいほど、ループを閉じたとき、システムは安定するんだよね。その値を位相余裕と呼んで、システムの安定性の目安にしているんだ

*比例＋積分要素のボード線図は第6回の図8を思い出してください。

よっしゃ、合格や。じゃあ、強風が吹いても目標位置から外れない自動走行システムを設計してもらおうか