車を思いのままに走らせるにはどうしたらいいの？：独学！ 機械設計者のための自動制御入門（3）（1/4 ページ）

曲がりくねった道の上からはみ出ないよう、自動車をうまく走らせる制御の仕組みってどうなっているの？

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

当連載の登場人物

銀二（ぎんじ）

設計コンサルタント。甥（おい）っ子の草太を自分の息子のようにかわいがっています。

草太（そうた）

銀二の甥。現在は大学院生です。ちょっと困るとすぐ叔父を頼ってしまうちゃっかり者だけど、頑張り屋さんです。

編集部注* 本記事はフィクションです。実在の人物団体などとは一切関係ありません。

　開ループシステムGoを閉ループにしてフィードバックシステムを構築すると、開ループシステムGoの特性によってはシステムが不安定となることがあります。今回は、そのメカニズムについて考えてみます。

開ループシステムについては、本連載第2回「猫とピンポン球と周波数応答特性』をご覧くださいニャー

いよいよ、自動制御理論も佳境に入ってきたな

開ループシステムGoのループを閉じると、システムが不安定となることがある。その原因が、Goの『情報や応答の遅れ』と『変化に対する過剰反応』であるってことは、車の運転の例で分かったよ。だけど、どのくらい“のんびり屋”、あるいは“慌てん坊”だと、コースから飛び出てしまうような不安定な運転になるのかが、どうもよく分からない

そうだろ、そうだろ。前回の説明で納得するようじゃ、技術者とはいえんな。今日は、その理屈を数学的に説明しよう

数学？ 数学を知らなくても理解できるといったじゃん！

高校で学習した数学ぐらい使わせてくれよ！

簡単に頼むよ

まず開ループシステムGo（図1）があるとする

図1　開ループシステム

そもそも開ループシステムGoが何を意味しているのか分からないんだよね。何をイメージすればいいのか分からない

それじゃあ、まずここでいう“システム”が何かっていうところから説明しようか。大部分の機器は入力を受けて何かを出力するやろ？ 例えばモータは電流を流せば軸が回転するから、入力は電流で、出力が軸の回転だ。あるいは電池をつなぐとモータは回転するから入力は電圧だと考えてもいい

モータの端子に電圧が掛かるとコイルに電流が流れるからだね？

そのとおり。だから入力を『X』、出力を『Y』とすれば、入出力システムを『Y＝G（X）』（出力は伝達関数に入力を掛けたもの）というふうに記述できる_*1やろ？

筆者注

*1 ここでは、Ｇは一般的な伝達関数を考えているので、開ループ伝達関数を意味する添え字oを付けていません。以下、Ｇに添え字oが付いているときは開ループ伝達関数、付いていない場合は一般的な伝達関数を意味していると理解してください。

出力Yは入力Xの関数として表現できるということだね

そういうことやね。制御ではGのことを、伝達関数と呼ぶのは知っているよな？ さらに、この伝達関数が大胆にも、

　G＝Y/X 　　（1）

出力を入力で割れば、伝達関数。

と書けるというところがミソだ。それで、システムというのは、この伝達関数がいくつもつながったもんだと考えたらええんや

う〜ん。もっと具体的に説明できないのかなぁ？

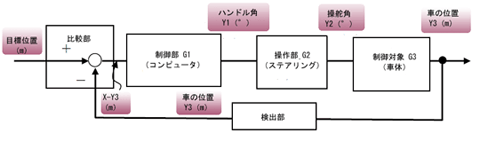
しゃーないなぁ。じゃあ、車の自動運転システムで具体的に説明してみようか（図2）

図2　自動運転制御の基本構成

　車を自動で運転するシステムというのは、車が道路の中央位置にくるように機械が自分でハンドルを操作するという機能のことや。つまり、道路の中央位置を目標位置として、そこに車体が来るように車体の位置を制御するということ。

で、この機能を実現するためには、ハンドルを駆動するモータおよびそのドライバや、車体の位置を検知するセンサ、ハンドル駆動モータを何度回転させればよいかを計算するコンピュータとその制御回路が必要となる。

それで、それぞれを伝達関数として表現して、模式図化して書くと図2のようになる。これが自動運転システムのブロック線図。

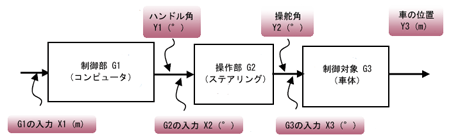
開ループシステムっちゅうのは、フィードバック回路を閉じる前のシステムっちゅうことや。具体的にいえば図3のブロック線図で示したのが開ループシステムや

図3　自動運転制御の開ループシステムGo

でも図1では開ループシステムGoは、1個の伝達関数で表現されてたじゃん

図1（再掲）

図3の制御部G1の入力は車体をX1 （m）横に移動させろ、という指令で、その出力はハンドルをY1（゜）回せという出力や。

このG1の出力Y1は操作部G2の、ハンドルをX2 （゜）回転させろという入力指令でもあるから、X2＝Y1だ。そして、X2対する出力としてタイヤがY2　（゜）回転する。同じく操舵角Y2は制御対象である車体の操舵角X3のことだからX3＝Y2だ。

車は進行方向に一定速度で走っている。最後のブロックはタイヤがX3 （゜）回転すれば、車体は進行方向に対して横にY3 （m）動くということをいっている。これらを、入力をX1、出力をY3としてまとめて書くと、

　　Y3/X1＝Y1/X1・Y2/X2・Y3/X3＝G1・G2・G3 （2）

『現在の車の位置』を『指令された移動量』で割ったGは、それぞれのシステムのGを掛けたものとなる。

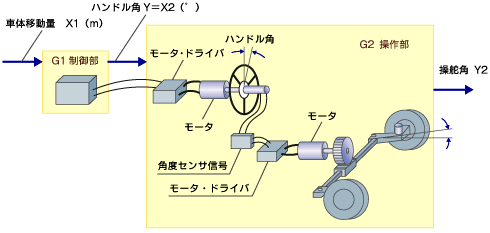
　……となる。各ブロックの具体的イメージは図4を見て、想像してほしい

図4　制御部の各ブロック イメージ

なるほど、システムというのは複数の機能を組み合わせた全体の機能あるいは構造を指し、図1の開ループシステムGoというのは、図2あるいは図3の個々の伝達関数をつなげたG1・G2・G3のことなんだね。

　各伝達関数が出力を入力で割ったものとして表現されているから、全体システムの入出力の比が、システムの内部のすべての伝達関数の積で記述することができるんだ。それで、最初のX1を入力すると、最後のY3が式（2）からパッと計算できる。

　つまり、開ループ伝達関数Goを使えば、車体の位置をX1（m）動かせっていう命令を受けたときに、車体が横方向に動く距離Y（m）が、

　　Y3＝Go・X1 （ただしGo= G1・G2・G3）　　　（3）

*『現在の車の位置』は『開ループ伝達関数』と『指令された移動量』を掛けたもの。

　で簡単に計算できる。これは確かに便利だね