変化のない人生と伝達関数は、あり得ない?:独学! 機械設計者のための自動制御入門(7)(1/4 ページ)
時間が十分経過したときの伝達関数の特性は、周波数応答特性で見れば低周波領域の特性に対応しているのはなぜ?
当連載の登場人物
銀二(ぎんじ)
設計コンサルタント。甥(おい)っ子の草太を自分の息子のようにかわいがっています。
草太(そうた)
銀二の甥。現在は大学院生です。ちょっと困るとすぐ叔父を頼ってしまうちゃっかり者だけど、頑張り屋さんです。
編集部注* 本記事はフィクションです。実在の人物団体などとは一切関係ありません。
今回は、今まで学習してきたことを復習しながら、静特性改善のための補償設計についての学習を仕上げます。第1回から主要なテーマとして取り上げてきた、車の自動走行の制御設計において、第5回で懸案となっていた、横風を受けて曲がる自動車をセンターラインに沿って真っすぐ運転させるためにはどうすればよいかという問題を解決します。
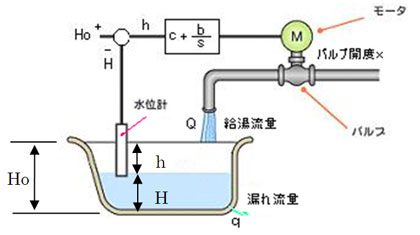
第6回では、その問題について考える前に、類型問題である、水漏れのある浴槽の水位を一定にする補償設計について検討しました。まずは前回の復習から始めましょう。
今回の解説も、瀬戸内海の風香る、銀二叔父さんの書斎からお届けします。銀二さんと草太は、朝から張り切って学習を始めます。
おはよう。昨晩はよく眠れたか?
明石海峡から涼しい風が吹いてくるから、気持ちよく眠れたよ
そうか、それはよかったな。早速だけど、昨日の復習をしとこか。水漏れのある浴槽の水位をどうやったら一定に制御できるか。目標水位Hoと実際の水位Hの差(偏差)h=Ho−Hに比例したバルブ開度xとする比例制御(図1のブロック線図でb=0)では、水漏れがある場合、水位Hを目標水位Hoまで到達させることはできへんかった。なぜならば、水漏れqに相当するお湯を補充するためのバルブ開度xを維持するためには、目標水位Hoとの偏差hが0であってはならないからやな
一方、偏差hが0となっても、漏れ流量qに相当するバルブの開度xを維持させるために、偏差hを積分する制御(図1のブロック線図でc=0)では、水位Hは目標水位Hoを中心にして変動するだけで、一向に目標水位に落ち着かへん。積分制御による浴槽水位制御の開ループシステムの位相余裕が0°やから、システムが不安定となるからやった。このことを、復習を兼ねて、基礎的なところから説明してくれへんかな?
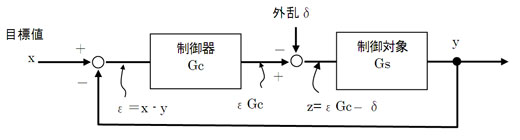
図2の外乱のある一般的なブロック線図で説明してみるよ。まず、システムの入力xと出力yの間の関係を次の伝達関数Gで表現することができる
図2のブロック線図のGsは制御対象の伝達関数だね。浴槽の水位制御であれば浴槽に給湯するお湯の量が入力で出力は水位。車の自動走行なら、タイヤの操舵角が入力で出力が車体の位置かな
ふむ、ふむ
Gcは、制御対象をコントロールするために必要なものの伝達関数だね。例えばコンピュータや、バルブあるいはハンドルやモータの特性だよ。ブロック線図と式(1)から、誰でも、次の3つの基礎式を立てることができる
数式が苦手な草太が、簡単に式を立てた。成長したなぁ
別に数学が苦手なわけじゃないよ。現実感のない無機質な数式が好きになれなかっただけで、現実と結びついた数式は嫌いじゃないよ。とにかく(2)〜(4)から……
いいぞ、いいぞ
Go=Gc・Gsとおくと(5)は
このGoを開ループシステムの伝達関数と呼ぶんだ。つまりループを閉じる前の入出力間の伝達特性を表しているんだ
フィードバック制御では、開ループ伝達関数Goの特性が重要な意味をもってくるんやな
そうなんだ。例えば比例制御の場合、偏差εに比例した値を制御対象Gsの入力とするってことだから、Gcは一定値だ。もしGsが∞ならば、Goも∞だから、(6)式は
となる。つまり制御器Gcを∞に設定しない限り、yは外乱δによって、目標値xからずれることになる
ところで制御対象の伝達関数Gsが∞ってどういうことやねん? 何かを入力したら出力が∞となる? そんなんでシステムとして成立するのか? そんなシステム存在するのか?
そんなこといったって、ここまでは叔父さんの受け売りだよ
自分の言葉で説明できなければ理解したとはいえんのやで
そういわれれば、そうだとは思うんだけどね……
草太は自分で考えてみました。
(7)までは、(1)を基礎として難しい計算でもないし、どこも間違っていません。でも、入力した途端、出力が∞となるようなシステムが存在するのか? 仮に存在するとして、そんなシステムは意味があるのか? と問われれば、そうも思います。
……Gsは伝達関数であって伝達率ではないよね。『伝達率』ならば一定値だから入力した途端、出力が∞となるシステムというのは違和感がある。けれど、通常は有限値だけれど、ある条件が満たされると∞となるシステムというのは、世の中にたくさんあるよ
代表的なのが共振だな
そうだよ! 共振がいい例だよ。つまり、システムは周波数に依存しているんだよ! システムの入出力の関係を意味している伝達関数も周波数に依存するんだ
『システムは周波数に依存している』って、なんか“格好いい表現”だけど、ちょっと抽象的やな。もっと具体的に説明できひんか?
第2回で、猫の目の前でピンポンをしたときの、猫の目がピンポン球を追いかけるアニメーションがあったでしょ。ピンポン球がゆっくり往復しているときは、猫の目は確実にピンポン球を捉えている。だけど、往復速度が速くなると追い付けなくなって、最後には瞳が動かなくなってしまった。あのアニメーションは、まさしく、『猫の目』のシステムの応答が周波数に依存しているってことを証明しているよ
思い出してくれたかにゃん?
つまり、システムの、入力に対する応答、つまり出力は、入力周波数に依存している、あるいは入力周波数の関数である、ってことやな
しょうゆーこと
なつかしいギャグやなぁ
それで、伝達関数の特性を、周波数応答特性曲線によって表現しているんだ
Copyright © ITmedia, Inc. All Rights Reserved.