試作品の数を劇的に減らす直交配列実験の実務:Excelで学ぶ実験計画法の基礎(3)(5/5 ページ)
品質管理のための代表的な統計手法である実験計画法について、実践的な手法を短期間に習得したいと希望している読者に向けて、Excelを使って効率的に独学できるような解説を行う。
直交表の特徴
直交配列実験を実施すると、どうして少ない実験回数で因子の効果を検証できるのでしょうか。最後に直交表の性質から、その理由を考察してみます。
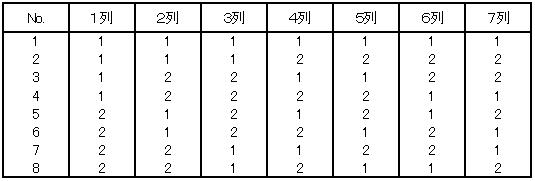
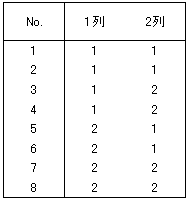
先のL8直交表を再掲します。
各列を変数と見なして、変数間の関係の強さを示す統計量、相関係数を計算してみます。相関係数は、−1から1までの値を取り、−1および1に近いほど2変数間の関係は強く、0に近いほど関係は弱いことを意味します。0のとき、2変数間にまったく関係はありません。相関係数が0、すなわち、まったく関係がないことを、統計では、「2変数は独立である」、または「2変数は直交している」と表現します。変数が複数ある場合は、ペアごとに計算した相関係数を相関係数行列と呼ばれるマトリックス表にまとめるのが一般的です。相関係数行列はExcelの分析ツール:相関(図10)を利用して計算できます。
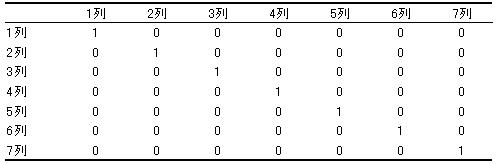
直交表の7列(=7変数)の相関係数行列を表7に示します。
対角線は、自分自身との相関係数で必ず1になります。各列の相関係数を見ると、すべて0、すなわち、各列は独立であり、直交していることが分かります。この性質が、直交表が“直交表”と呼ばれる所以(ゆえん)です。直交していると、各列の効果を独立に議論できるようになります。どういう意味かは、各列が独立でない場合で説明します。
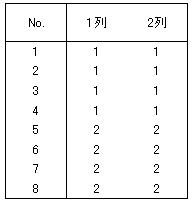
1列と2列の数値の配列を表8のように変えます。数値1、2の出現数は4つで同じですが、各行の数値は同じ値になっています。この2つの列の相関係数行列は、表9のとおりです。
2列の間には、片方の列の数値が1のとき1、2のとき2で、片方の列の数値が決まれば、もう片方の列の数値が完全に決まる関係にあります。よって、統計的に最も関係の強い状態になり、相関係数は1になります。元の直交表ではどうでしょう(表10)。
片方の列が1のとき、もう片方の列の数値は1と2が同数、すなわち50%の確率で出現しています。片方の列が2のときも同様です。すなわち、片方の列の値が分かっても、もう片方の列の数値を特定することができません。水準(1と2)ごとに見た、もう一方の条件の出現率が等しいときは、統計的な予測が不可能(どちらかの数値がランダムに出現するとしかいえない)な状態であり、2つの列は無関係、すなわち独立です。表現を変えると、各列は相互に影響していないともいえます。影響していないので、各列の効果を独立に検証できるのです。
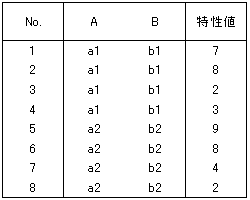
一方、関係している状態、先に数値の配列を変えた表8で実験を計画して、表11のようなデータが得られたとします。
各列の水準(数値1、2)ごとの特性値の平均値を計算すると、当然ですが、同じ値になります(表12)。
しかし、この結果からは、因子Aによって、特性値に違いが出たのか、因子Bによって、特性値に違いが出たのかは分かりません。因子Aの水準がa1のときb1、水準がa2のときb2となり、完全に対応しているからです。このような状況を因子が交絡しているといいます。因子が交絡している実験で得られたデータからは、特性値に影響する要因を特定することはできません。
一方、直交表の各列は無相関であり、実施した実験で取り上げた因子間に交絡はありません。すなわち、直交表を利用すると、無駄のない効率的な実験が計画でき、かつ、各因子の水準の平均値の差から因子の効果が検証できるのです。以上、直交表の性質を簡単に説明しました。
今回は、利用頻度の高い2水準系の直交表で、直交配列実験および直交表の特徴を紹介しましたが、2水準に限らず、3水準や4水準の直交表も準備されています。また、すべての因子が同じ水準でない混合型の直交表も準備されています。直交配列実験は、商品企画や設計の場における品質管理のツールとして利用価値の高い方法です。ぜひ、活用してみてください。
◇
次回が最終回になります。最終回は、これまで紹介した方法のおさらいと、そのほか、実務の現場で実施されている、応用的な実験とその解析方法を紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.