有限要素法は解析要素がバネだと考える:仕事にちゃんと役立つ材料力学(5)(3/3 ページ)
バネの伸びは加えられた力に比例する。伸びた分が「ひずみ」である。部品がバネであると考えればひずみと応力の関係も理解しやすい。
フックの法則〜応力とひずみの関係〜
さてここまでで、応力とひずみのイメージが皆さんのアタマの中に出来上がったと思います。僕がこの連載を通して伝えたいことの約半分は終わりました。次回は応力とひずみの関係を解説しますが、そのための予習として、今回はバネと重りについて解説しておきたいと思います。
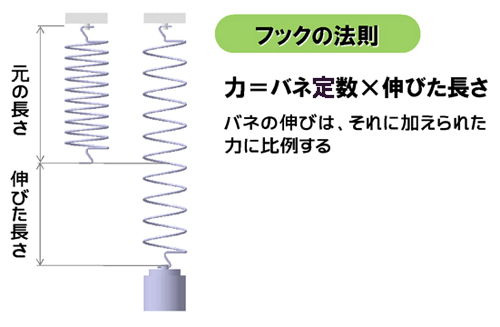
皆さんは「フックの法則」って覚えていますか? いまの教育では、理科でやるのか、物理でやるのか、ちょっと分からないのですが……。教科書ではつるまきバネと重りの絵が必ず使われて説明されているはずです。この絵だけは見覚えがある、という方が多いのではないでしょうか(図5)。
感覚的に理解できるシンプルな法則です。実はこれにはとっても深い意味があるのです。つるまきバネの上端を天井に固定して、下端にゆっくりと重りをぶら下げると、バネが伸びます。そして、重りを取り去ると、バネは元の状態に戻ります。
もちろん重りが重過ぎるとバネが伸び切ってしまい、重りを取り去ってもバネは元の長さに戻らなくなります。フックの法則は「重りを取り去ったときに、バネは元の長さに戻る範囲」の重りであることが条件となっています。
この前提条件を基にして考えると、重り(=力)をぶら下げると、その分バネは伸びます。その伸び率は、バネの強さによって決まってくるのですが、そのバネの強さを「バネ定数」といいます。そして「重りの重さとバネの伸びる量は比例する」というのがフックの法則です。
僕はこの連載の初回でもお話ししたとおり“材料力学ダメ人間”でしたので、社会に出てからこの式をあらためて見たとき、実は「つまらない法則だなぁ」と思ってしまいました。だって、まず上で解説したような制限があるでしょう? 万有引力の法則のような基本法則とは明らかに違う法則なのに、“法則”という名前が付いていることが不思議に思えました。
「フックの法則ってすごい!」と思ったのは、有限要素法の基礎理論を学んだときでした。「有限要素法は、解析する要素をバネと考えればいいんだ!」と分かったときに、フックの法則の偉大さが理解できました。
そんなことを考えながらブラウジングしていると……いるんですねぇ、僕と同じことを思っている人って(以下URL)。
僕は解析工房のとき、「すべての部品は、金属タワシのようなバネのカタマリです」といっているのですが、この人も「すべてのモノはバネである」といっておられました。
。oO 筆者のつぶやき
ニュートンに消された男・フック
法則には人の名前が付いていることが多いですよね。フックの法則もそうです。こういう人名が付いた法則を見ると、僕は「この人ってどんな人だったんだろう?」と思いをめぐらせてしまいます。
ニュートンとか、レオナルド・ダ・ヴィンチはとっても有名なので、逸話もたくさん紹介されていますし、生い立ちも簡単に調べられます。ところがフックくらいだと、そうそうたくさんの資料はありません。解析工房を一緒に企画したお客さまがフックについて調べてくれたので、ここで紹介しましょう。
フックはイギリスの物理学者です。生物学者でもあり、細胞を見つけた人のようです。また画家を目指したくらい絵が上手です。彼の描いた虫のスケッチを見ましたが、すごいです。さらに建築家としても活躍したようです。ダヴィンチといい、昔の人は多才ですね。ボイルの法則という法則を聞いたことがあると思いますが、この“ボイル”もまた人名です。そして、その弟子がフックでした。そしてボイルの法則とは、本当はフックが発見した可能性が大きいそうです。
つまりフックは、先生のボイルに「成果を横取りされた!」ということになります。また彼は、望遠鏡の開発にも携わった天文学者という顔も持っていたようです。同世代の学者にかの有名なニュートンがいます。フックには「ニュートンに消された男」という別名があるそうです。
ニュートンと万有引力の法則の先駆権を争ったからです。結果は皆さんがご存じのとおり、ニュートンが勝ちました。ボイルに成果を横取りされ、ニュートンに先を越されたことによって、そうなったのか、どうなったのか、彼は攻撃的で他人の業績にケチをつけて論争を挑むことの好きなイヤな性格だったようで、自分の論敵をこっぴどく攻撃したようです。その攻撃たるや半端なものではなく、ニュートンは彼が亡くなるのを待ってから学説を発表したほどです。
◇
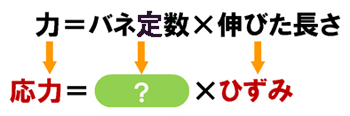
応力も力の一種、ひずみも“伸びた長さの一種”なんだと割り切って、フックの法則を置き換えてみましょう! (図6)
さてこの場合、「バネ定数」は何になるのでしょう? 次回は、応力とひずみの関係を探りながらこの問いを解き明かしていきましょう。(次回に続く)
*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***
Copyright © ITmedia, Inc. All Rights Reserved.