有限要素法は解析要素がバネだと考える：仕事にちゃんと役立つ材料力学（5）（2/3 ページ）

バネの伸びは加えられた力に比例する。伸びた分が「ひずみ」である。部品がバネであると考えればひずみと応力の関係も理解しやすい。

[栗崎 彰／キャドラボ，MONOist]

変形があって、ひずみがある

　さて、構造や部品に力が掛かると応力が発生するのですが、同時に起こるプロセスとして、変形があります。

　材料力学の世界では、この変形を「ひずみ」というもので表現します。「ひずみ」は、材料力学を理解するために、応力と同様にとても大切な概念です。今回は「ひずみ」を理解しましょう。ひずみは応力と同時に発生します。ひずみが発生しているのに、応力が発生していないとか、応力が発生しているのに、ひずみが発生してないとか、そういうことはありません。

　さて、またまたイメージの時間です。身近なモノで感触が分かっているものとして、円柱の形をした消しゴムを例に挙げます。

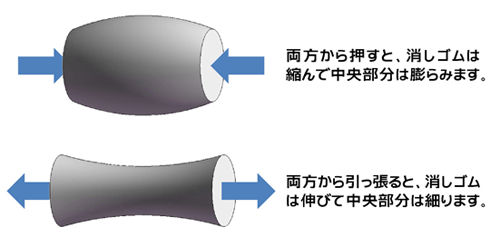
　消しゴムを親指と人さし指で挟んで持って、グィっと押してみましょう。両側から押さえられた消しゴムは押された方向に縮んで、中央が少し膨らみますね。

　今度は消しゴムを両側から引っ張ってみましょう。両側から引っ張られた消しゴムは引っ張られた方向に伸びて、中央が少し細くなりますね。

　これは消しゴムなので、肉眼でも変形は見ることができますね。これが鉄やアルミなど金属では見ることはできませんが、同じような形状に変形しています（図1）。

図1　円筒状の物体の両端を押したり引っ張ったりすると？

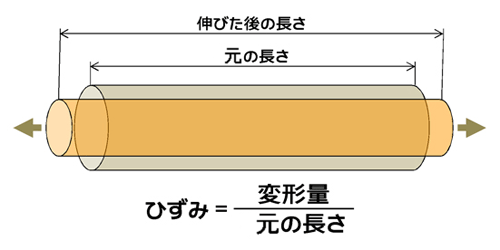
　「ひずみ」とは力を受けたときの変形量を元の長さで割ったものです。つまり元の長さに対して、縮んだり伸びたりした変形量の割合がひずみになります。ひずみの単位ですが、長さを長さで割っているので、単位がありません（図2）。

図2　ひずみとは？

　金属材料などのひずみは、非常に小さく、1×10-6ミリメートルとかそれくらいのオーダーです。ひずみは計測することができます。ひずみゲージと呼ばれるものを実験するモノに張ってひずみを計測します。

• ひずみとは（東京測器研究所）

垂直ひずみとせん断ひずみ

　ひずみも応力と同じように成分があります。応力のときと同じように、皆さんの設計している部品から“極限に小さい”サイコロを切り出して考えてみましょう。もちろん部品には何らかの力が掛かっています。そしてその極限に小さいサイコロには変形してひずみが発生し、応力が発生しています。応力を説明した3次元のサイコロで描くとゴチャゴチャしてしまうので、今回は平面的な図で表現してみました。

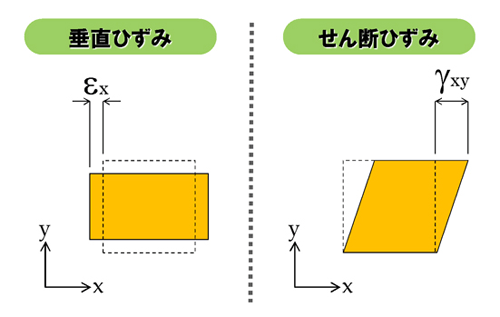
　そのサイコロを真横から見てみると、ひずみはこの図のような成分に分解できるはずです（図3）。

図3　ひずみの成分　「垂直ひずみ」と「せん断ひずみ」

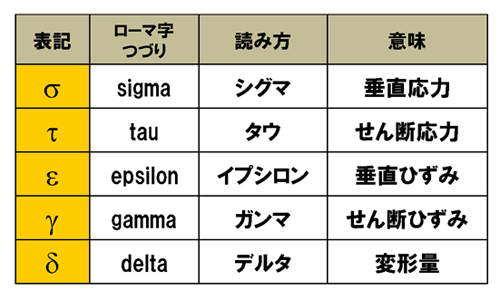
　垂直ひずみはε（イプシロン）、せん断ひずみはγ（ガンマ）で表現されます。応力に続き、またまたギリシャ文字の登場です。老婆心ながら、材料力学に使われるギリシャ文字をまとめておきますね（図4）。

図4　ギリシャ文字の意味一覧