電線に流すことができる電流値を求める：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（6）（2/3 ページ）
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第6回は、円筒座標系の熱伝導方程式を解き、電線に何アンペアまで流せるかを求める。
電線に流すことができる電流値
設計条件として「絶縁被覆が焦げたり溶けたりしないように、被覆の最高温度が40［degC］以下であること」とします。Excelの「ゴールシーク機能」を使って、被覆の最高温度T1がちょうど40［degC］となるように電流値を求めました。表2に計算結果を示します。
図2に導体径と電流値の関係を示します。
以前、コイルの設計をしていた際、会社の先輩に導体の断面積について質問したことがあります。その答えは「1スケ1アンペアかな」でした。要するに、電流密度を1［A/mm2］にしてはどうかということです。電流を2倍にする場合は導体断面積も2倍、導体径は√2倍ですね。つまり、導体径と電流値の関係は放物線となります。図2に放物線を記入しておきました。流せる電流と放物線は重なりません。ここでの結論は以下の通りです。
電線に流すことができる電流値は、導体断面積に比例（導体径の二乗に比例）するものではない。多くの電流を流したい場合、導体断面積は電流値の上昇分よりも大きくする必要がある。
比例関係でないことは「電線便覧」を見れば分かってもらえると思います。反対のことを言うと、細い電線には案外大きな電流を流せます。
図3は筆者が自宅で試作中の電気回路です。真空管のヒーターには1本当たり0.6［A］ほどの電流が流れます。真空管が3本あるので2［A］弱の電流が流れますが、ブレットボードや導線はかなり細い割に熱くなりませんでした。
熱伝導と同じ振る舞いをする物理現象
微分方程式の形が同じであれば、境界条件が異なっても同様の答えが得られます。ここでは、熱伝導の他に導体内部の電位と電流密度、地下水の流れを紹介します。ポアソンの方程式は以下の形をしています。連載第2回の式39の時間変化がない場合です。
式8の右辺をゼロとしたものがラプラスの方程式です。それらの特徴は、スカラー量であるポテンシャルを座標xで微分したものをベクトルのx方向成分、座標yで微分したものをベクトルのy方向成分、座標zで微分したものをベクトルのz方向成分とすると、それらが意味を持つ量になると記憶しています。
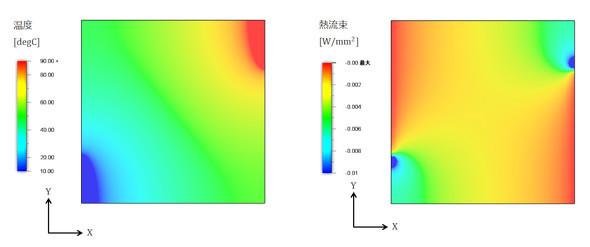
熱解析では、温度がポテンシャルに相当し、熱流束がベクトル量に相当します。これを式で表すと以下となります（式9）。
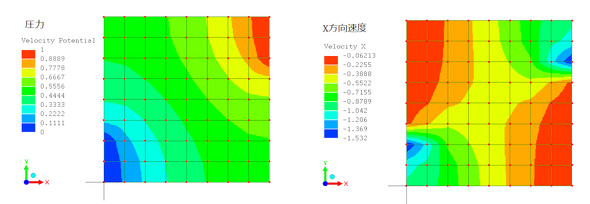
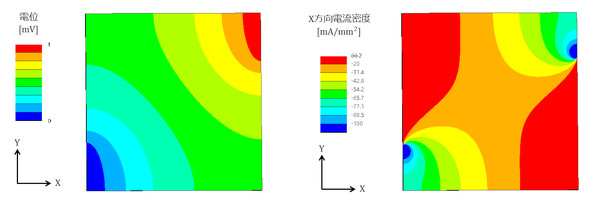
図4に熱解析によって求めた温度と熱流束を、図5に地下水の流れであるポテンシャル流れを、図6に導体内の電位と電流密度を示します。いずれも同じ結果となります。ということは、熱解析ソフトがあればポアソンの方程式で支配される他の解析ができることになります。
Copyright © ITmedia, Inc. All Rights Reserved.