溶接部の疲労強度（その1）：CAEを正しく使い疲労強度計算と有機的につなげる（10）（3/5 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第10回は「溶接部の疲労強度」について取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

S-N曲線

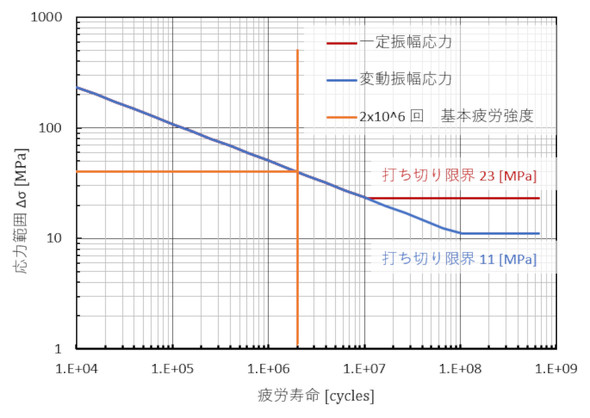
　式6の応力範囲の打ち切り限界Δσ_ceを説明します。溶接継手にもS-N曲線があります。図9に溶接継手のS-N曲線の例を示します。例えば、応力範囲が40［MPa］のときの寿命は2×10⁶［cycles］となります。そして、応力振幅が一定値の場合、応力範囲が23［MPa］よりも小さければ半永久的に壊れないことになります。応力振幅が変動する場合は、11［MPa］よりも小さければ半永久的に壊れないことになりますが、応力振幅が変動するときは考え方が複数あります。

図9　溶接継手のS-N曲線［クリックで拡大］

　図9の2×10⁶［cycles］のときの強度と打ち切り限界の応力レンジは、完全溶け込み溶接、すみ肉溶接、荷重伝達型、荷重非伝達型で異なる値となります。S-N曲線は式8で表されます。

式8

　本連載の中で、「安全率が1［-］で破壊確率50［％］、設計では安全率を2［-］以上」と説明しましたが、今回の安全率は大きくても1.25［-］です。この理由を説明します。

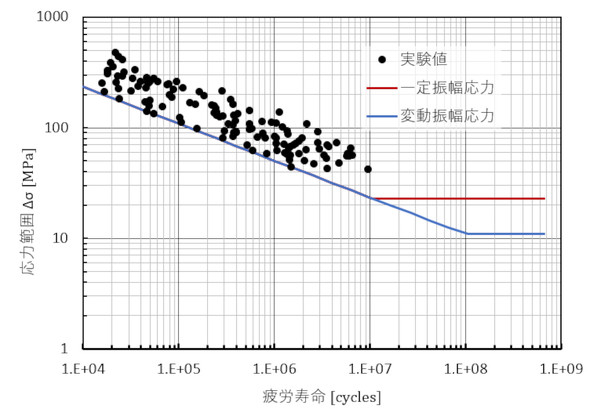
　まず、溶接部の疲労強度は大きくバラツキます。実験値で2倍、3倍のバラツキが出るのは普通です。筆者の手元のデータでは、溶接継手の疲労強度は母材の疲労強度の2分の1のデータもあれば、5分の1のデータもあります。図10は参考文献［1］のデータを見て筆者が勝手に作ったイメージ図です。式8の定数はバラツキのあるプロットの下限で決めているところがポイントです。式8は破壊確率が50［％］ではなく、かなり0［％］に近いと思っております。このような理由から安全率は大きくても1.25［-］でよいとされていると推測しています。

図10　溶接継手のS-N曲線：実験値をプロット［クリックで拡大］

　あと一つ言えることは、溶接継手の実験データは公称応力で整理されていることです。この結果、比較すべき応力は公称応力となります。図2の応力集中部の応力ではないのです。

参考文献：

• ［1］日本鋼構造協会｜鋼構造物の疲労設計指針・同解説｜技報堂出版（2014）

応力振幅が変動するとき

　応力振幅が変動するときの手順を説明します。線形累積損傷側を使います。簡単な例を使いましょう。通常の応力レンジは30［MPa］で、たまにドカーンと大きな応力レンジ80［MPa］が作用するケースを想定します。応力レンジと荷重回数を以下に記します。

• 荷重1：Δσ₁＝80［MPa］，n₁＝1.0×10⁴［cycles］
• 荷重2：Δσ₂＝30［MPa］，n₂＝2.0×10⁶［cycles］

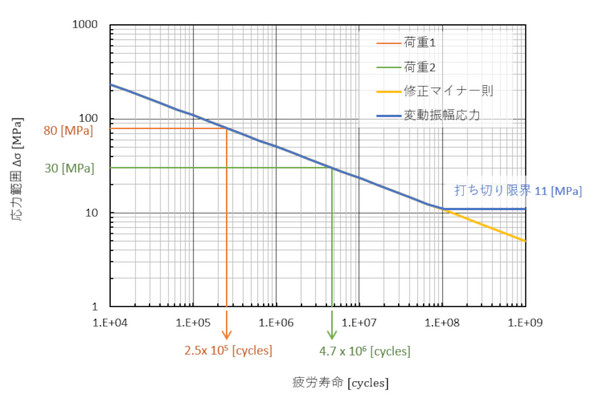
　次にS-N線図を使って、上記応力レンジが作用したときの寿命を求めます。図11のような感じです。

図11　溶接継手のS-N曲線：寿命を求める［クリックで拡大］

• 荷重1の寿命：N₁＝2.5×10⁵［cycles］
• 荷重2の寿命：N₂＝4.7×10⁶［cycles］

　次の式9が成立すれば、溶接部は大丈夫となります。

式9

　数値を代入しましょう。式9が成立するので溶接部はOKとなります。

式10

　応力範囲が打ち切り限界を下回った場合は、3通りの考え方があります。1つ目は「損傷度合いはない」という考え方で、式11となります。この考え方を使う場合、半永久的に壊れないとの判断がされます。

式11

　2つ目は、S-N曲線を延長する方法です。これを「修正マイナー則」といいます。図11の黄色の線です。そして、3つ目はその中間のようなものです。これらの考え方では半永久的に壊れないとの判断ができません。