溶接部の疲労強度（その1）：CAEを正しく使い疲労強度計算と有機的につなげる（10）（2/5 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第10回は「溶接部の疲労強度」について取り上げる。

LINE

Hatena

簡単な例

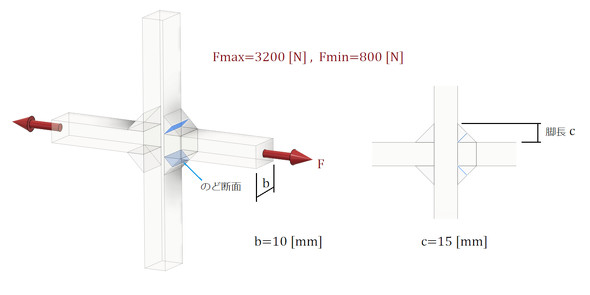
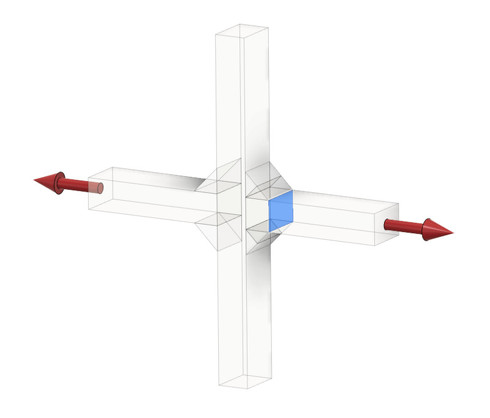
　簡単な例を使って強度計算の流れを説明します。この強度計算のことを「公称応力を用いた疲労照査」といいます（参考文献［1］）。公称応力を使うので、応力は「力／断面積」です。ルート部（溶接ビード）の断面は図6に示したのど断面です。図6の場合、次式となります（式1）。

図6　ルート部の断面［クリックで拡大］

式1

　図7に止端部の断面を示します。止端部の断面は分かりやすいですね。

図7　止端部の断面［クリックで拡大］

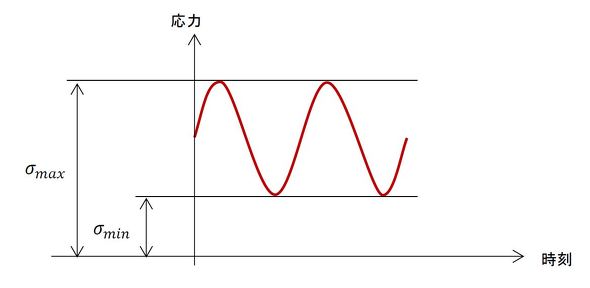
　次は、応力レンジです。図8に応力の変化を示します。応力レンジは式2で定義されます。

図8　応力の変化［クリックで拡大］

式2

　応力振幅の倍になることに注意が必要です。両振荷重ならばCAE解析で出た応力値を2倍する必要があります（たまに2倍するのを忘れてしまいます）。

　では、数値を代入しましょう。図6の寸法を使って、のど断面と止端部の面積は以下の式となります（式3、式4）。

式3

式4

　止端部の断面積が小さいので、止端部の評価をします。荷重Fの最大値を3200［N］、最小値を800［N］とすると、止端部の応力レンジは以下となります。

式5［クリックで拡大］

　参考文献［1］によると、式6を満足すれば「簡便な疲労照査」は完了です。つまり、疲労破断はしないと判断できます。

式6

　式6に数値を代入します。

式7

　式6を満足しました。詳細は文献を参照していただくとして、大体こんな感じです。