フローで考える熱のモデリング（その3） 〜ドライヤーを例に熱のモデリングを行う〜：1Dモデリングの勘所（33）（2/4 ページ）

「1Dモデリング」に関する連載。連載第33回では「フローで考える熱のモデリング（その3）」と題し、ドライヤーを例に熱のモデリングを行う。

[大富浩一／日本機械学会 設計研究会，MONOist]

パラメータの決定

　次に、各要素のパラメータを決定する。

ヒーター

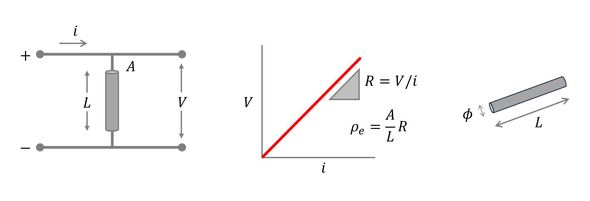
　棒状の材料の電気抵抗Rは、棒の両端の電位降下Vを、棒を通過する電流iで除した式（オームの法則）

式7

で表現され、抵抗は電流が導体（棒）を通過する際に消費されるパワー（単位時間当たりのエネルギー）

式8

を決定する。これを「ジュール熱」という。抵抗に関する物性である電気抵抗率ρ_eは次式で定義される。

式9

　Aは棒の断面積、Lは長さである。以上の関係を図4に示す。

図4　ヒーターの性質と形状［クリックで拡大］

　ヒーターは図4右図に示すように直径Φ［m］、長さL［m］の丸線形状のニクロム線とする。今、このニクロム線に電圧Vを印加すると抵抗体を流れる電流によってジュール熱が発生する。ここでオームの法則を使ってジュール熱を表現すると、

式10

となる。ρ_e［Ωm］は電気抵抗率で、ニクロム線の場合はρ_e＝1.079×10^-6Ωmである。なお、ここでジュール熱を1kW一定とすると、

式11

となる。すなわち、電気抵抗Rは一位的に決まるので、

式12

となる。

ファン

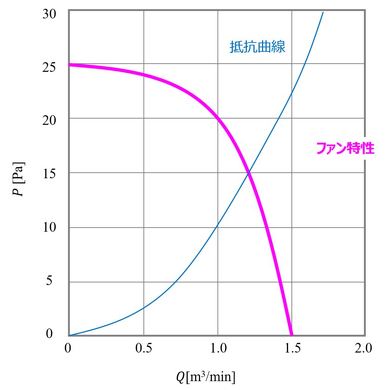
　ドライヤーで使用するファンとして、図5に示す特性のファンを想定する。

図5　ファン特性［クリックで拡大］

ヒーターと流れ間の強制対流熱伝達

　ヒーター（円柱物体）と流れ間の強制対流熱伝達は経験的に、

式13

となることが知られている（参考文献［1］）。ここに、

式14

で、G＝hA、A＝1／2πΦL（円柱の半側面で熱伝達が行われるとして）であるから

式15［クリックで拡大］

となる。この式を整理して、ヒーターと流れ間の強制対流熱伝達による熱コンダクタンスは、

式16

となる。λは空気の熱伝導率で0.03W/m・K、νは動粘性係数で15×10^-6m²/s、c_pは比熱で1000J/kg・K、また、粘性係数はμ＝ρνで、密度ρは0℃のとき、1.293kg/m³である。