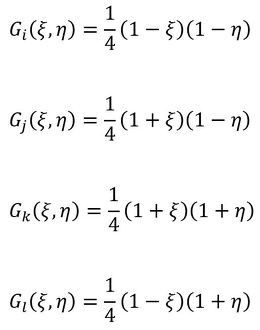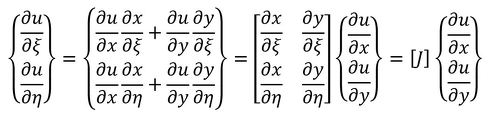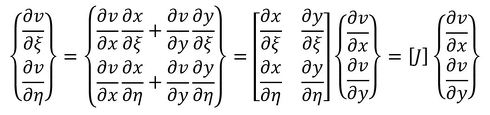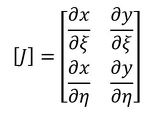有限要素法入門 〜要素剛性マトリクスの導出〜:CAEを正しく使い疲労強度計算と有機的につなげる(4)(4/7 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第4回は、前回に引き続き「有限要素法」について解説する。
おまけ:アイソパラメトリック要素
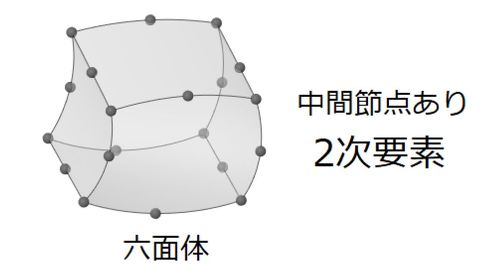
2次元四角形要素と3次元六面体要素の要素剛性マトリクスについて説明します。要素剛性マトリクスはどのような要素でも式26と式27で求まりますが、図4に示す20節点六面体要素を考えてみましょう。
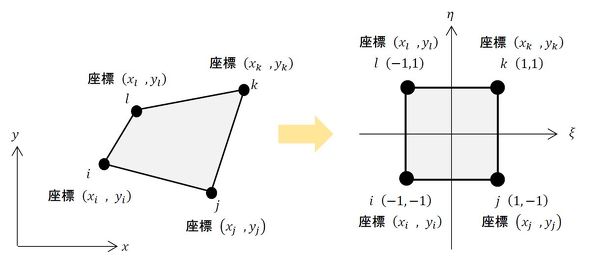
6つの面は曲面です。これを体積積分するのですが、やる気が出るでしょうか……。出ませんね。座標変換して体積積分を簡単にしましょう。取りあえず2次元四角形1次要素から始めます。図5に示したように、1辺の長さが2[m]の正方形に座標変換します。
座標変換のための式は次式となります。
左下のi節点に注目します。ξ=−1、η=−1のとき、式28の左辺と右辺の値はxiとならなければなりません。ということは、Gi(−1,−1)=1となってもらい、それ以外のG(ξ,η)はゼロとなってもらうと都合がいいです。次式となります。
右下のj節点に注目します。ξ=1、η=-1のとき、式28の左辺と右辺の値はxjとならなければなりません。ということは、Gj(1,−1)=1となってもらい、それ以外のG(ξ,η)はゼロとなってもらうと都合がいいですね。次式となります。
k節点、l節点も同様に考えると、G(ξ,η)は次式となります。
式29、式31、式33、式34を満たすG(ξ,η)は次式となります。
変位u、vがx、yの関数で、座標x、yがξ、ηの関数であるとき、u、vの微分は次式で表されます。
マトリクス[J]は次式で定義しました。
Copyright © ITmedia, Inc. All Rights Reserved.