解析ソフトは使わずに「Excel」で実験モーダル解析をやってみる：CAEと計測技術を使った振動・騒音対策（12）（5/6 ページ）

“解析専任者に連絡する前に設計者がやるべきこと”を主眼に置き、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。連載第12回では「『Excel』を用いた実験モーダル解析」について取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

モーダル解析のまとめ

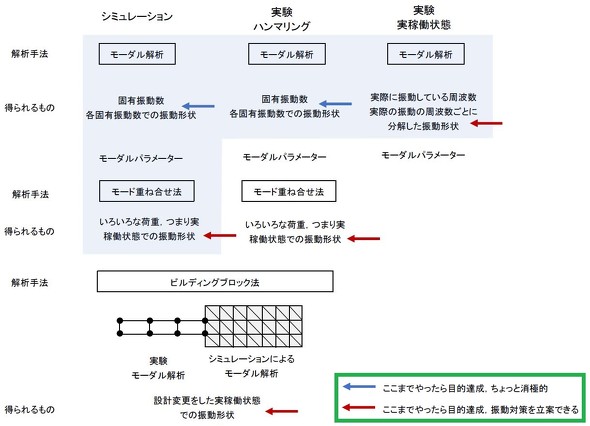
　前回と今回でシミュレーションと実験のモーダル解析を説明しました。まとめたものを図18に示します。

図18　モーダル解析のまとめ［クリックで拡大］

　図18の水色で網掛けした領域は、本連載で既に説明したか、これから説明するものです。図中のモーダルパラメーターは、対象物の振動特性を表す等価的な質量、ばね定数、減衰係数と、固有振動数とモードシェイプなどで、これらを使うといろいろな加振力に対する振動応答を求めることができます。モーダルパラメーターはシミュレーションだけでなく、実験からも求められます。

　また、「ビルディングブロック法」と呼ばれる手法があり、いくつかのユニットのモーダルパラメーターが分かっていたら、それらを組み合わせた状態の振動応答を求めることができるようです。図のように、あるユニットのモーダルパラメーターは実験から求め、あるユニットのモーダルパラメーターはシミュレーションから求めて、全体の振動応答を求めることが可能とのことですが、筆者はここまでの経験を持ち合わせていませんので紹介だけにしておきます。

　矢印記号は着地点です。青色の矢印（←）まで進めたらひとまず目的達成です。しかし、ここで得られた情報からは「装置が将来共振状態になるかどうかが分かる」程度であって、振動低減のための施策のヒントは得られず、少し消極的な目的達成です。さらに、赤色の矢印（←）まで進められれば、振動低減のための施策を立案できるように思えます。

振動形状の3次元表示

　3次元表示した振動形状は、グルグル回すことで3次元的な立体として認識できます。動画1／動画2のようにExcelのグラフ（散布図）で3次元表示をしましょう。振動形状において時々刻々と移動する測定点の位置は3次元的なもので、x座標、y座標、z座標を持っていますが、散布図はx座標とy座標だけです。ここでは散布図のx座標とy座標を求めることを目標とします。

　今さらですが、ベクトルの内積と外積をおさらいしておきましょう（ベクトルは斜体太字で表記します）。ベクトルの内積は式8でした。

式8

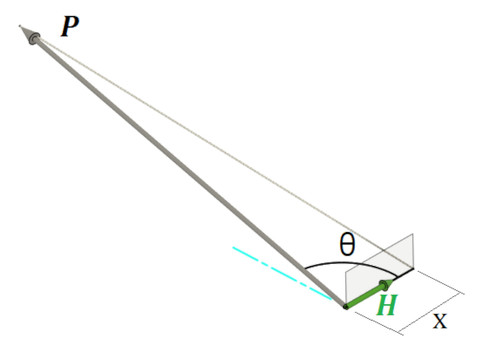
　図19において、PベクトルとHベクトルの内積からPベクトルのHベクトル方向成分xを求めることができます。式9となります。

図19　ベクトルの内積［クリックで拡大］

式9

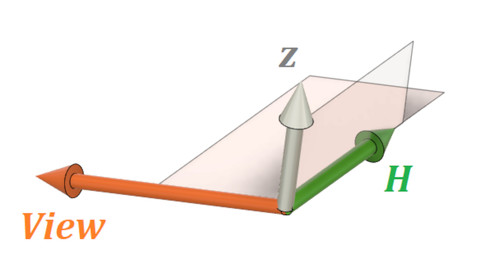
　図20において、Viewベクトルとzベクトルの外積はHベクトルとなります。

図20　ベクトルの外積［クリックで拡大］

　式10で表記しますが、ここではViewベクトルとHベクトルが直交することと、zベクトルとHベクトルが直交することだけを利用します。

式10

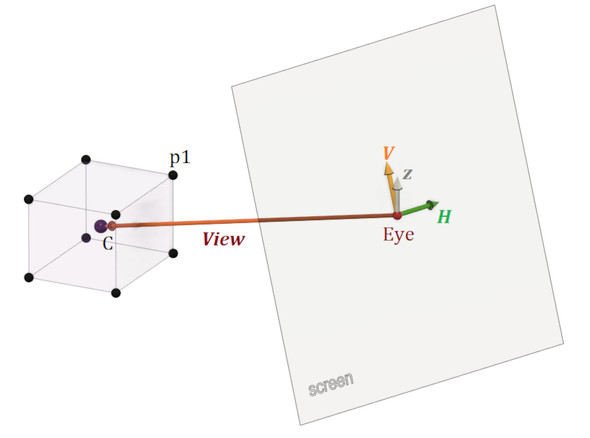
　図21に計算するための座標とベクトルを示します。

図21　計算するための座標とベクトル［クリックで拡大］

　p1は測定点の位置です。式7を使ってx方向変位、y方向変位、z方向変位を計算します。Cは中心で、C点の座標は各測定点の座標の平均値です。Eyeは視点です。ここで、表示する画面の天地を決めましょう。zベクトルが上を向くとします。zベクトルの成分は（0，0，1）でよいでしょう。Viewベクトルは見る方向で、Cの座標からEyeの座標を引き算すれば求まります。