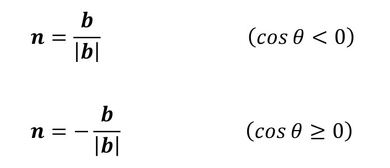領域最適化のアルゴリズムについて考える：フリーFEMソフトとExcelマクロで形状最適化（12）（4/6 ページ）

原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる！　本連載ではフリーのFEM（有限要素法）ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第12回では、前回に引き続き「領域最適化」をテーマに具体的なアルゴリズムについて考えながら、その理解を深めていく。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

法線ベクトルの計算

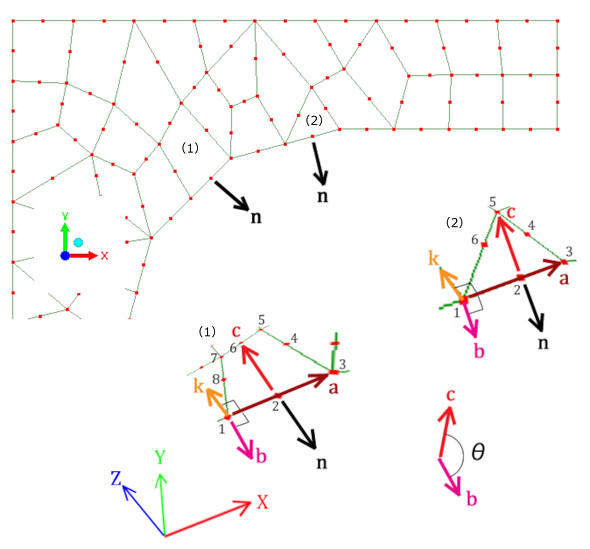
　次に、法線ベクトルの計算法を説明します。図8のような有限要素法モデルがあったとします。8節点四角形要素（1）と、6節点三角形要素（2）の境界線の法線ベクトルを求める計算式を導きましょう。

図8　法線ベクトルの求め方［クリックで拡大］

　図8の要素（1）の境界線上にある節点2の法線ベクトルnを求めます。節点1から節点3へ向かうベクトルをaとします。aは次式で決まります。

式7

node1_x、node1_y、node3_x、node3_y：節点座標　
i：x軸に平行な大きさ「1」のベクトル
j：y軸に平行な大きさ「1」のベクトル

　2次問題なのでx座標とy座標しかないのですが、z座標を導入します。ベクトルkをz軸に平行な大きさ「1」のベクトルとします。aとkの外積bはaと直交し、かつkとも直交します。kと直交するということは、bはxy面内にあるということになります。そして、aと直交するということは、bは法線ベクトルの候補となります。次式です。

式8

　節点番号は図8の順番に付けられているはずですが、念のためbの方向を確認していきます。ベクトルcを次式で求めます。cは要素表面で必ず内側を向いているベクトルです。

式9

　ベクトルの内積を復習します。ベクトルの内積の大きさは次式で計算されましたね。

式10

式11

　θが90［deg］を超え、180［deg］以下ならば、つまりcosθがマイナス値だったら、bは要素の外側を向きます。何かの間違いでcosθがプラス値だったらbの向きを反転させます。次にbの大きさを「1」とするために、|b|で割り算すると、法線ベクトルnが求まります。次式です。

式12