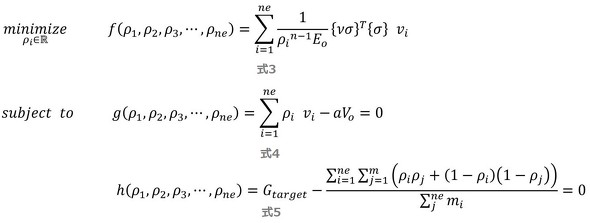チェッカーフラグ対策付きトポロジー最適化の実践：フリーFEMソフトとExcelマクロで形状最適化（10）（2/4 ページ）

原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる！　本連載ではフリーのFEM（有限要素法）ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第10回では、チェッカーフラグ対策付きトポロジー最適化を実践するとともに、対策のないトポロジー最適化結果との比較を行う。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

片持ちはりのトポロジー最適化の続き

　ρ_iの濃淡の図の変化を図6に示します。チェッカーフラグはなくなりました。第7世代くらいで将来有望な小骨がありましたが消えてしまい少し残念です。

図6　片持ちはりのトポロジー最適化の密度の変化［クリックで拡大］

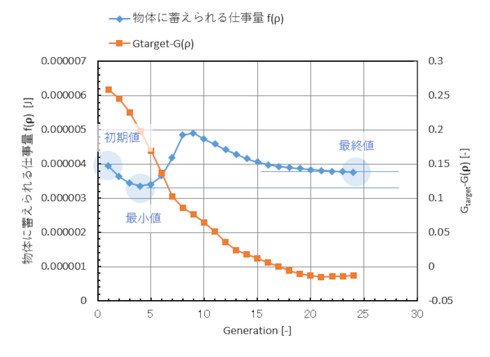
　図7に、物体に蓄えられる仕事量f（ρ）と制約関数h（G_target−G（ρ））の変化を示します。仕事量fが第4世代で最小値を示し、その後増加してまた小さくなっていきました。第4世代の密度ρが中間的な値なので、軽石のようなスカスカの素材で作れば、平均コンプライアンスが最小、つまり剛性が最大になると解釈できます。しかし、軽石状の部品を設計するのは都合が悪いですし、ExcelシートのAX列を見るとチェッカーフラグの度合いを示す数G（ρ）が目標値に達していません。第4世代以降が最適化の本番となります。

図7　物体に蓄えられる仕事量と制約関数「h＝G_target−G（ρ）」の変化［クリックで拡大］

　図5のオレンジ色グラフは、制約関数h（G_target−G（ρ））の変化です。第20世代以降でほぼゼロになっています。つまり、第2の制約条件式5が満たされています。連載第9回で述べたフィードバック系が機能していると考えられます。第1の制約条件式4は常に満たされているので、第20世代以降で、以下の問題が解けたことになります。

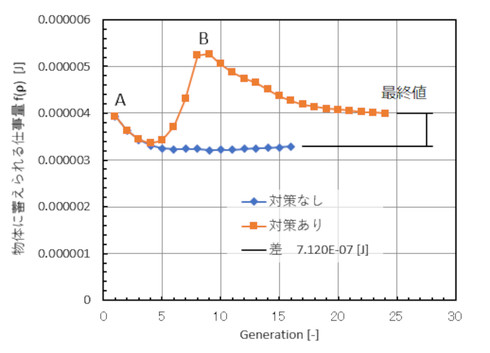
　それでは、チェッカーフラグ対策をしていないトポロジー最適化結果と比較してみましょう。図8に密度ρ_iの分布、図9に物体に蓄えられるエネルギーの比較を示します。チェッカーフラグ対策をすると、小骨がなくって製品にしやすい形になりましたが、ゼロ戦の設計者である堀越二郎が見たら「サバの骨ではない」と言うのでしょうか。

図8　密度ρiの分布の比較［クリックで拡大］

　図9を見ると、最終世代の物体に蓄えられるエネルギーに差が出て、小骨がないと剛性が低下する結果となりました。対策ありの蓄えられるエネルギーの最終値が図のA点とあまり変わらないことが気になります。そもそもA点の密度ρは0.375［-］と中間的な値でスカスカな軽石です。スカスカな軽石はラティス構造であって、「軽くて石のように硬い」ので、そこそこ剛性が高く最適化解なのです。最適化はB点が始点と解釈しています。

図9　物体に蓄えられる仕事量の比較［クリックで拡大］