1Dモデリングの方法にもさまざまなアプローチがある：1Dモデリングの勘所（4）（2/3 ページ）

「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。

[大富浩一／日本機械学会 設計研究会，MONOist]

直接類比モデリング

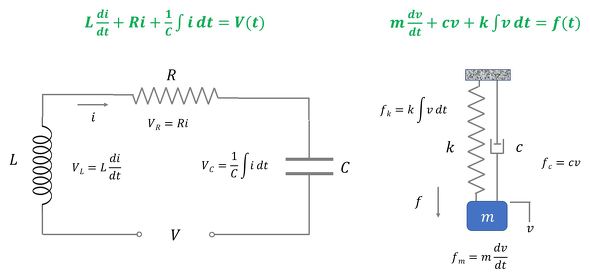
　直接類比表現による電気系と機械系の比較を図6に示す。既に述べたように、支配方程式は両者で同じであるが、対象とする物理モデル（図で表現したモデル）では違いがあることが分かる。電気系では、各素子（要素）が直列につながっているのに対し、機械系では並列につながっている。

図6　直接類比（Direct Analogy）［クリックで拡大］

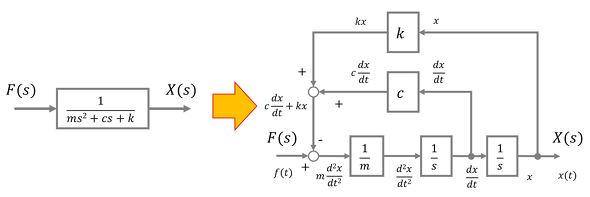
　すなわち、直接類比では支配方程式が同じ形式で表現されるために、その解法は例えば図7のブロック線図による解法のように、電気系でも機械系でも同じである。一方、解く際には入力（図7の場合は力）を決めて、変位（速度）について解くことになる。また、図表現では類推が全く効かなくなる可能性があり、解析ツールとして構成しようとすると問題が生じる。

図7　ブロック線図による直接類比モデルの解法［クリックで拡大］

逆類比モデリング

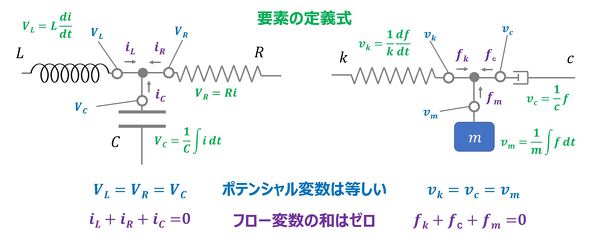
　逆類比では、1ページ目の図5右図の対応関係を用いる。図8に逆類比による電気系と機械系の類推を示す。機械系の要素の定義式に違和感はあるものの、図表現としての電気系と機械系の類推は成立しており、“ポテンシャル変数は等しい”“フロー変数の和はゼロ”といった対応もできている。

図8　逆類比（Inverse Analogy）［クリックで拡大］

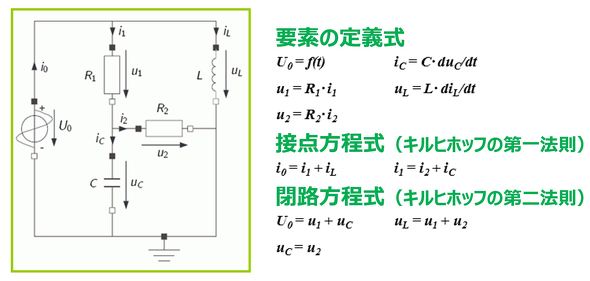
　図8の関係を用いて、ある電気回路を表現した例を図9に示す（参考文献［2］）。10個の未知数に対して、10個の関係式（要素の定義式、接点方程式、閉路方程式）となり、微分代数方程式として解くことができる。

図9　微分代数方程式による逆類比モデルの解法（参考文献［2］から引用）［クリックで拡大］

参考文献：

［2］CellierFrançois. Lecture note of ‘Mathematical Modeling of Physical Systems’, Department of Computer Science, Swiss Federal Institute of Technology（ETH） Zurich.2012

直接類比モデリングと逆類比モデリング

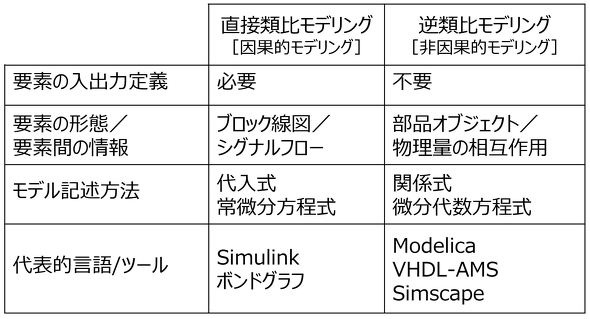
　以上、類推モデリングに関して、直接類比と逆類比について説明した。両者の比較を表1に示す。両者それぞれ長所／短所があり、目的に応じて両者を使い分けすればよい。

　1Dモデリングでは、言語として「Modelica」を使用する場合があり、表1に示すように逆類比を採用している。逆類比は直感的に理解しづらい面もあるが、類推モデリング自体が便宜的な方法であると理解した上で、割り切ってその仕組みを把握しておくことが重要である。

表1　直接類比モデリングと逆類比モデリングの比較［クリックで拡大］