位置度を考える上で重要な「最大実体公差」の「動的公差線図」：産機設計者が解説「公差計算・公差解析」（14）（2/4 ページ）

機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第14回は、位置度を考える上で重要な最大実体公差の「動的公差線図」について取り上げる。

[土橋美博／飯沼ゲージ製作所，MONOist]

動的公差線図について

　続いて、ガタ（部品と部品の隙間）と幾何公差域の関係をグラフとして表すことができる「動的公差線図」について説明します。

　では、穴について考えてみます。穴の最大実体状態は、穴径が最も小さい状態です。前回使用した図を例に、動的公差線図を描いてみます。まずは、最大実体公差方式を使用せずに、位置度公差Φ0.1［mm］のみを使用した場合です。

図3　位置度公差のみの場合の動的公差線図 ［クリックで拡大］

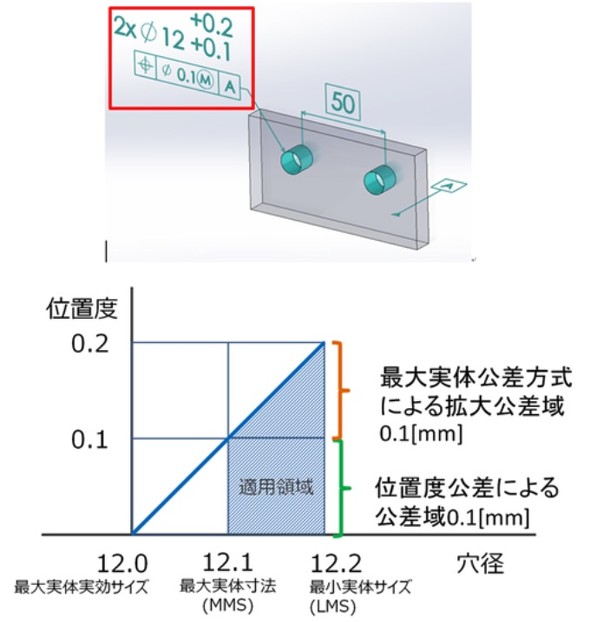
　図3において、穴径はサイズ公差領域より、Φ12.1〜12.2［mm］の範囲で利用できることが示されています。

　次に、最大実体公差方式の場合について、動的公差線図を描いてみます。

図4　最大実体公差方式の場合の動的公差線図 ［クリックで拡大］

　この場合、図3に対して、最大実体実効サイズを起点に、最小実体サイズまで直線を伸ばします。その結果、位置度公差のみの場合と比べ、「位置度がΦ0.2［mm］に拡大できたこと」が表されています。この動的公差線図から、位置度公差のみの適用に比べて、最大実体公差方式の場合は「適用領域が1.5倍になっている」ことが分かります。

　これが何を示しているのかといえば、

位置度の規格が拡大されることで、

・幾何公差の理論上の最適化が図れる
・規格が緩和されて歩留まりが向上する
・コストダウンが可能となる

ということです。

　公差設計／公差解析／加工完成品の実態調査を行えば、さらなる最適化も可能です。