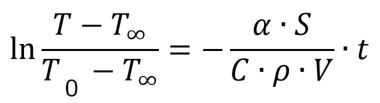強制対流による冷却を考える：初心者のための流体解析入門（11）（3/4 ページ）

流体解析をテーマに、入門者や初学者でも分かりやすくをモットーに、その基礎を詳しく解説する連載。今回のテーマは“強制対流による冷却”だ。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

流速と熱伝達率の関係を考える

　さて、ここから考えていきたいのは、“どのくらいの時間で、どの程度温度を下げたいのか”という目標を実現するためには、「どの程度の熱伝達率が必要なのか」、さらにその熱伝達率を実現するには、「どの程度の流速が必要なのか」という“当たり”の部分です。

　ここを考えておかないと、例えば「どのようなファンで、どの程度の空気を送ればよいのか」ということも、当てずっぽうになってしまいます。

　ということで、ここからその関係について考えていきます。

　まず、熱伝達率αと流速U_∞の関係を考えます。前述の式を用いることで、以下のように表せます。代表長を0.01m（10mm）としたとき、

式9　代表長を0.01mとした場合の熱伝達率と流速の関係式

となります。

　なお、レイノルズ数が5×10⁵よりも大きい場合は、もう1つの式を使いますが、今回の例ではレイノルズ数が小さいため、こちらは割愛します。この式では、目的の熱伝達係数を得るための流速の見積もりが可能です。

　しかし、これだけでは、目的の時間内に、初期温度からターゲット温度まで下げることができるのか分かりません。

　そこで、熱伝達率と温度の関係を考えてみます。そのためには、非定常伝熱のための計算式を考えてやる必要があります。ここではその詳しい説明は割愛し、今回の目的の式を示します。Cを比熱（J/kgK）、密度をρ（kg/m³）、Vを物体の体積（m³）、Sを物体の表面積（m²）、αを熱伝達率（W/m²K）、tを時間（s）、Tを温度、T_∞を雰囲気温度、T₀を初期温度としたとき、

式10　非定常伝熱のための計算式

とすることができます。

　ここから、任意の温度や材料物性、時間などを代入することによって、目的の時間とターゲットとなる温度に対する熱伝達率を求めることができます。後は、この熱伝達率と流速の関係を求めてやればよいことになります。