さまざまな幾何公差【その1】〜その定義や例、測定方法について〜：産機設計者が解説「公差計算・公差解析」（6）（2/3 ページ）

機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第6回は“具体的な幾何公差”について取り上げる。

[土橋美博／飯沼ゲージ製作所，MONOist]

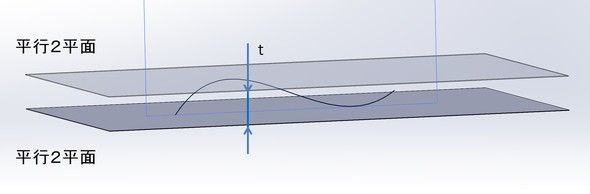
1-1-2．円筒表面の真直度公差

公差域の定義

　円筒表面上にある任意の実際の線は、「t」だけ離れた「平行2平面」によって規制されます。

平行2平面による規制

3次元モデルによるイメージ

例

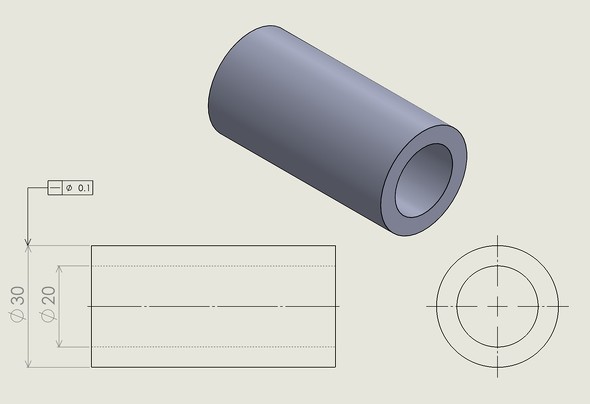
　円筒表面上にある任意の実際の線は、「0.1」だけ離れた平行2平面の間になければならない図面で表しています。

2D図面での例（円筒表面の真直度公差）

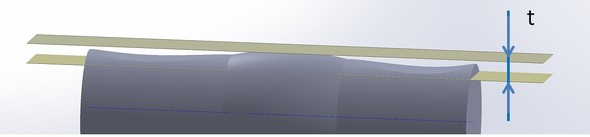
測定方法

　平面の真直度公差と同じ測定方法になります。

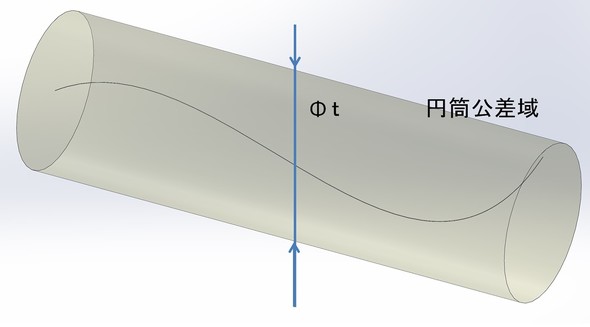
1-1-3．円筒軸線の真直度公差

公差域の定義

　公差値の前に記号Φを付けると、公差域は直径「t」の「円筒」によって規制されます。

直径tの円筒による規制

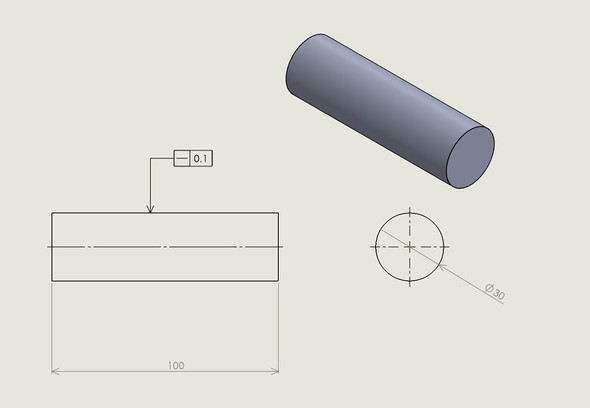
例

　円筒の実際の軸線は、直径「0.1」の円筒公差域の中になければならないことを図面で表しています。

2D図面での例（円筒軸線の真直度公差）

測定方法

　部品を回転させ、円周方向の振れの値を測定します。測定した振れの半分の値における最大差が円筒軸線の真直度となります。

　真直度公差を円筒に適用する場合、その語句から「同心度」「同軸度」「円周振れ」などと混同してしまうことはないでしょうか？　筆者は少し混乱することがあります。詳細はこの後に説明しますが、同軸度公差は、データム軸直線と同一直線上にあるべき軸線のデータム軸直線からの狂いの許容値を示し、同心度公差は、データム円の中心に対する他の円形形体における中心の位置狂いの許容値を規定する位置公差になるので、ここまで説明したデータムを必要とせず、単独で形体を規定する形状公差とは取り扱い方が異なります。