位置公差、輪郭度、振れ公差の測定はどうやるのか：寸法を実感する！ 測定講座（6）（1/2 ページ）

今回は複合位置度公差について解説した後、位置公差、輪郭度、振れ公差の測定方法について説明する。

[木下悟志／プラーナー，MONOist]

　前回は、幾何公差の最大効果をもたらし、他の幾何公差の多くをカバーできる位置公差に関して説明しました。今回は、まず複合位置度公差という便利なものを紹介します。続いて、位置公差、輪郭度、振れ公差の測定方法について解説していきます

複合位置度公差でスッキリ

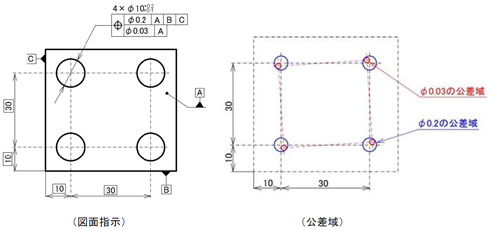
　図1は同じサイズ寸法（Φ10）を持つ複数の形体に対して、同じ位置度公差を指示し、かつ2種の位置度公差を同時に指示しています。

図1：複合位置度公差の例

　非常に便利なものですからぜひ覚えてください。まず図1左、2階建てになっている公差指示の上段、Φ0.2の公差指示ですが、データムがA・B・Cとなっています。これは、Φ10の穴の中心がAに直角で、B、Cからそれぞれ、四角で囲んだ寸法の位置においてΦ0.2の円筒公差域の中に入らなくてはならないことを表しています。

　そして特徴的なのが、下段のΦ0.03の公差指示です。これはデータムがAのみです。実は、これはデータムB，Cとは無関係で、データムAに直角に、4つの穴同士の30と指示された中心距離のみを規制するものなのです。その公差域はΦ0.03の円筒公差域なのです。それを図示したのが、右図の公差域の図です。この方法の利点は、見てお分かりの通り、図中に寸法矢印が少なく、かつそれぞれの矢印に公差指示がないので、図面が非常にスッキリすることです。

　また、中心距離への公差指示をデータムB、Cと分けて考えることができ、さらに形体数がどれだけあっても1つの公差指示枠で指示することが可能です。ここでは直交方向の複数形体でしたが、回転方向に配された複数形体にも適用できます。その場合は、位置を指示する寸法はピッチ円直径と角度になります。

　では、どういったところに使われるかということですが、図1の例では、例えば、これが4本の足を持ったモーターの受け台としたら、モーターの足を挿入するΦ10の穴は、データムB，Cに対しては厳しい位置公差は不要ですが、モーターの足の中心距離関係は厳しくしないと、正確にモーターの位置を決められない場合などに適用できます。従来は、位置決め精度のみを考えて、データムB，Cからの位置公差も厳しくしていたケースが多かったのではないでしょうか。

位置度の測定

　位置公差の測定ですが、データムからの距離を測定する、かつデータムが派生形体、すなわち中心軸や中心平面となることが多い、と考えると、測定機には中心位置を求めるための演算装置が必須です。実は、幾何公差の効果を最も発揮する位置公差の普及は測定機の進化と普及に依存しているのです。近年、徐々にそういった演算機能を有する測定機の普及が進んできており、いよいよ新しい時代の到来を感じさせるものがあります。一方、位置度測定に関しては、上記のように中心位置を測定することが圧倒的に多いため、従来のノギスやマイクロメータのような汎用測定機では測定不可能と言い切っても過言ではないのです。

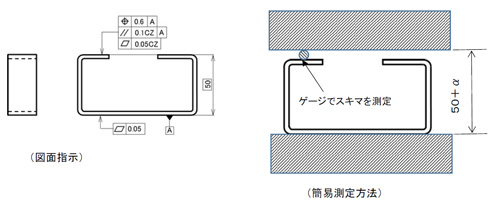
　図2のように無理やり、ゲージなどを用いて簡易的に測ることは可能ですが、基本的には輪郭度も含めて、位置公差は3次元測定機か演算機能を持った画像測定機（工場顕微鏡含む）を必要とします。

図2：位置度の簡易測定例

　50＋αのスキマを設定した治具を用い、ワークと治具との間のスキマをゲージにて測定しますが、ゲージがΦαであれば位置度の公差値に対する偏差はゼロになります。

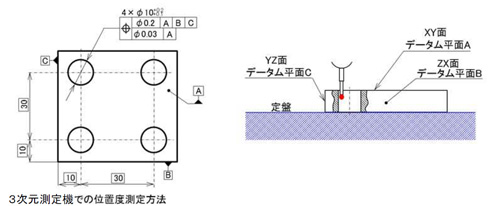
　図1に類する位置度測定には、3次元測定機を用いて、図3のように測定します。

図3：3次元測定機による穴位置の位置度測定

図3について補足

　まずデータム面にプローブを当てて直交座標系を設定する。次に、4つの穴にプローブを当てて測定する。

　最近販売されている3次元測定機では幾何公差を検証するソフトが組み込まれている。そのため、図3左の部品において、4つの各穴について位置度の検証結果を出力させられる。また穴の深さを変えて数カ所測定することにより、円筒度や直角度、真直度などの検証結果として出力することも可能だ。

　3次元測定機を新規導入する場合は、幾何公差への対応や出力などの仕様について検討が必要である。