幾何公差って測定はどうなるの？：寸法を実感する！ 測定講座（1）（2/3 ページ）

近年、幾何公差の普及の必要性が求められているが、製造する側ではその測定方法への課題が大きく、幾何公差に対応した測定技術の普及との同調なくして成立しないというのが現実である。本連載では幾何公差や寸法測定の課題に対する幾つかの取り組みを紹介していく。

[木下悟志／プラーナ―，MONOist]

本連載のトライアルワーク

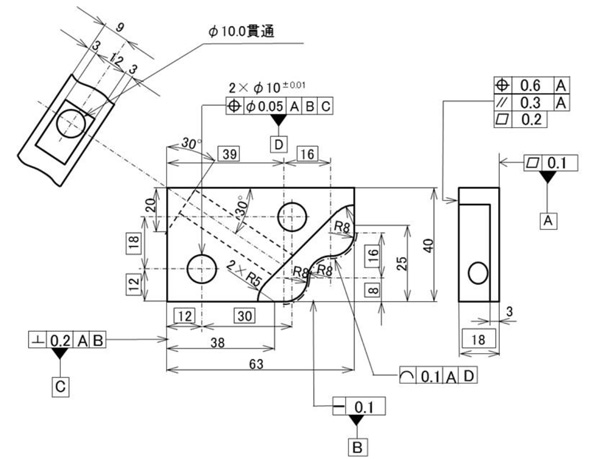
　第1回の今回は、私どもが設計した、図2のトライアルワーク（教材）の紹介をします。

図2：トライアルワーク

　今後、この図を用いてアルミの切削で製作したワークと私どもで所有している3Dプリンタで製作した樹脂ワークを、さまざまな測定機を用いて、ここに指示した各種幾何公差を測定して行きます。

　今回は、記載された幾何公差の概要を説明します。次回以降は、各幾何公差の特徴、目的、測定方法などを説明していき、実際に測定したデータの事例も提示します。

　まずは、ざっと図面を眺めていただいた第一印象はどうですか？

　何となくすっきりとした図面になっていませんか。今までの図面で見慣れた±とかの公差指示があまり見当たらないと思います。そうなのです、幾何公差では従来の寸法公差図面と異なり、形体（図形の要素、面、線、円、軸、点）などの大きさや位置を示す数字を□で囲んで「理論的に正確な寸法」として、そこに指示する公差は、別に公差指示枠というもので示します。ですから、個別の寸法には公差値が書き込まれていないので、すっきりしています。図面中□でかこまれた数値を見つけたら、どこかに幾何公差指示がされていると考えて探してください。

　次に、「▲」で示した記号に目がいきませんか？

　これは、「データム」といって、幾何公差の生命線ともいうべき記号です。これは、姿勢公差、位置公差、振れ公差の基準となる形体を指示するもので、従来も平行度や直角度（垂直度という人も多いですが、今後は直角度と呼んであげてください）、同軸度などの基準として、注記で指示されていたと思います。

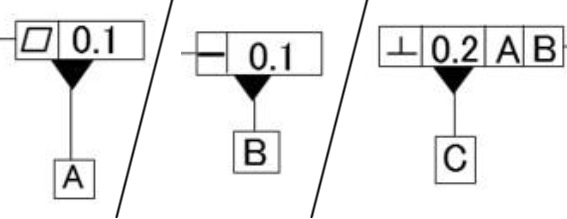
　なお、基準となるデータムには「基準としての精度」を求めることが理想的で、ここの例では、データムAには平面度、データムBには真直度、データムCには直角度といった公差の指示をしています（図3）。それぞれの公差については、次回以降に説明します。

図3：A〜Bのデータム図示