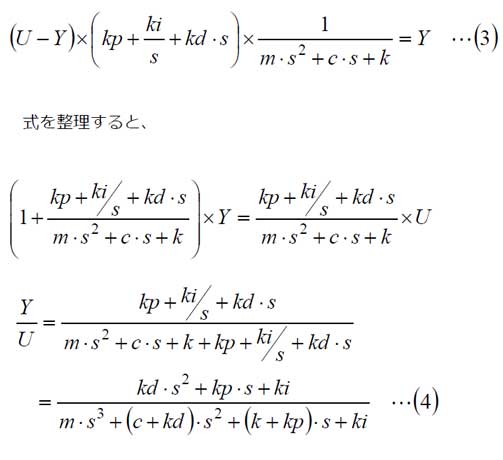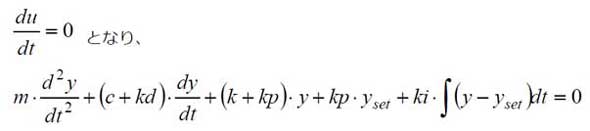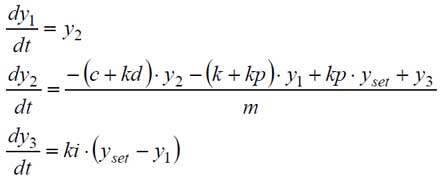ブロック線図を使ったPIDコントローラーのシミュレーション:無償ソフトで技術計算しよう【制御工学基礎編】(3)(2/3 ページ)
今回は、数式で表されたモデルを信号の流れとして可視化する「ブロック線図」と呼ばれる手法について説明する。
一次遅れ系、二次遅れ系
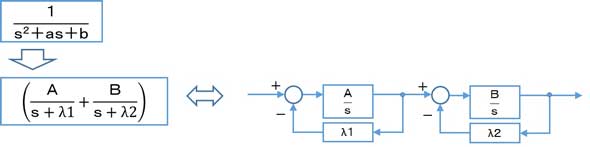
同様にして、一次遅れ系のブロック線図を作成すると、図8に示すように、積分要素と比例要素との組み合わせになります。
演算子法では、sを掛ける操作は微分操作を、sで割る操作は積分操作を、定数を掛ける操作は比例操作を表します。従って、ブロック内に「s」とあるのは微分要素、「1/s」とあるのは積分要素、例えば「a」などの定数があるのは比例要素と呼びます。
同じく、二次遅れ系をブロック線図で表すと、図9に示すように、2つの一次遅れ系の直列接続で表されます。
このように、最小要素まで分解できるものを線形制御系と呼び、古典制御理論は線形制御系を対象としています。
PIDコントローラー
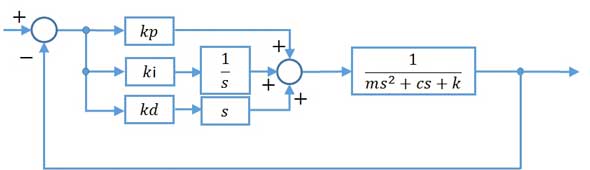
では【制御工学基礎編】(1)で紹介したPIDコントローラー付のバネ・マス・ダンパ系のブロック線図を作成し、伝達関数を求めてみます。次いで、伝達関数を微分方程式にして、FreeMatでシミュレートしてみます。
PIDコントローラーは比例要素、積分要素、微分要素からなるもので、制御対象の前段に置いて、フィードバックループを構成して使用します。従って、比例定数をkp、積分定数をki、微分定数をkdとすると、ブロック線図は図10のようになります。
このブロック線図から伝達関数を求めてみます。
便宜上、入力をU、出力をYとすると、フィードバックした結果とPIDコントローラーと制御対象との伝達関数の積が出力Yとなるため、以下の式が成り立ちます。
となり、(4)式のように伝達関数が求まります。この伝達関数を基に、応答性や安定性を評価します。詳細については、応用編で説明します。
さて、(4)式の伝達関数にysetの入力を与えた場合の応答をFreeMatで計算してみましょう。
(4)式を下記のように変形します。
演算子法では、sのべき乗は高階微分,1/sは積分になるため、
となります。ここで、入力uはyset(一定値)であるため、
となります
FreeMatのode45で計算するには1階の微分にしなければならないため、y1、y2、y3を導入し、下記のように変形します。
となり、これは【制御工学基礎編】(1)でバネ・マス・ダンパ系にPIDコントローラーを追加した際の考え方と同じ式になります。
Copyright © ITmedia, Inc. All Rights Reserved.