無償ソフト「FreeMat」で制御工学を学ぼう:無償ソフトで技術計算しよう【制御工学基礎編】(1)(1/2 ページ)
制御工学は数式が多く、分かりにくい分野の1つ。今回は無償ソフト「FreeMat」で制御の様子を疑似的に体感しながら、学習していこう。
| FreeMatでエンジニアリング計算: | |
|---|---|
| ⇒ | 入門編 |
| ⇒ | グラフィックス編 |
| ⇒ | プログラミング基礎編 |
| ⇒ | プログラミング処理編 |
| ⇒ | プログラミング応用編 |
| ⇒ | シミュレーション基礎編 |
| ⇒ | シミュレーション応用編 |
今回から制御工学編です。伝達関数やブロック線図、ボード線図などについてを基礎として3回に渡って説明し、次いで、応答特性や安定性についてを同じく3回に渡って解説します。制御工学は数式が多く、分かりにくい分野の1つです。そこで、本連載では、前回のシミュレーション編で行ったように、FreeMatで数式モデルを計算させることで、制御の様子を疑似的に体感できるようにします。今回は、バネで支えられた物体を所定の位置に移動させる際の制御について、FreeMatのシミュレーションを用いて説明します。
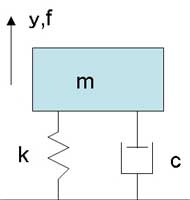
図1はシミュレーション応用編(3)で説明したバネ・マス系モデルです。
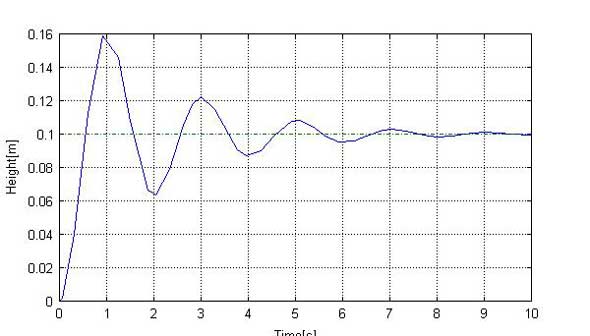
ここで、質量mをysetだけ持ち上げることを考えます。静止した状態では、バネはバネ定数×変位の力を発生するので、バネ定数k、目標の変位ysetとして、荷重f=k*ysetで引っ張れば良いことが分かります。質量m=1[kg]、バネ定数k=10[N/m]、減衰係数c=1[Ns/m]として、変位を計算すると、図2が得られます。
計算に用いたプログラムは下記のex501.mです。詳細はシミュレーション応用編(3)を参照してください。
clear;
c=1;k=10;m=1;yset=0.1;
f=k*yset;
dydt=@(t,y) [y(2);(f-c*y(2)-k*y(1))/m];
[t,y]=ode45(dydt,[0,10],[0;0]);
plot(t,y(:,1),t,yset*ones(length(t),1),'-.');grid('on');
xlabel('Time[s]');ylabel('Height[m]');
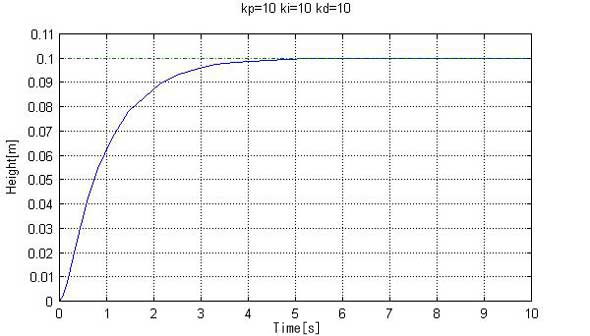
図2を見ると、最終的に目標とする値yset=0.1に落ち着きますが、目標値を大きく上回り、ついで下回りといった具合に、大きく変動しています。そこで、変位を検出してPIDコントローラーで制御を行ってみます。PIDコントローラーは検出された状態量(この場合、変位)を基に、比例(Proportional)・積分(Integral)・微分(Differential)動作を行い、目標値に速やかに到達するように、操作量(この場合は荷重)を制御する装置です。ex501.mにPIDコントローラーを組み合わせて、変位を計算したものが、図3です。
図3にkp=10、ki=10、kd=10とあるのが、PIDコントローラーの比例定数、積分定数、微分定数で、対象に合わせて設定する必要があります。図を見ると、非常に滑らかにかつ、速やかに目標値に到達していることが分かります。PIDコントローラーが幅広く普及している実情を考えると、驚くようなことではありませんが、図2と図3を比べると、制御技術がいかに大切であるかが、分かるかと思います。
下記のex502.mが、ex501.mにPIDコントローラーを組み合わせたものです。
clear;
c=1;k=10;m=1;yset=0.1;
kp=10;ki=10;kd=10;
dydt=@(t,y) [y(2);(kp*(yset-y(1))-kd*y(2)+y(3)-c*y(2)-k*y(1))/m;ki*(yset-y(1))];
[t,y]=ode45(dydt,[0,10],[0;0;0]);
plot(t,y(:,1),t,yset*ones(length(t),1),'-.');grid('on');
xlabel('Time[s]');ylabel('Height[m]');
title(['kp=',num2str(kp),' ki=',num2str(ki),' kd=',num2str(kd)]);
ex501.mでの荷重fの代わりに、ex502.mでは、kp*(yset−y(1))-kd*y(2)+y(3)を与えます。ここで、y(1)は変位で、比例動作は、目標値との差、「yset−y(1)」に定数kpを掛けたものを荷重として加えます。微分動作は、「yset-y(1)」の微分、つまり−y(2)に定数kdを掛けたものを荷重として加えます。
また、積分動作は、「yset−y(1)」の積分、
に定数kiを掛けたものを荷重として加えます。積分はそのままでは扱えないので、微分して、y(3)=ki×(yset−y(1))として、連立微分方程式の1つとして、dydtで定義される関数に与えます。
kp、ki、kdに適当な値を入れて、ex502.mを動作させると、変位のプロフィールが得られます。
図3のkp、ki、kdは筆者が適当に設定した値なので、もっと良い値が見つかるかもしれません。試してみてください。
Copyright © ITmedia, Inc. All Rights Reserved.