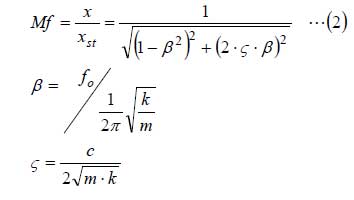振動問題をFreeMatで解いてみよう(その2):無償ソフトで技術計算しよう【シミュレーション応用編】(3)(3/3 ページ)
今回はバネ・マス・ダンパ系の方程式を無償ソフト「FreeMat」で解いてみる。
強制振動
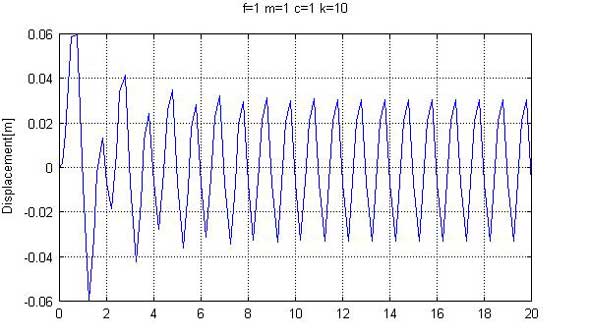
エンジンや回転機械のように、一定周期で振動するものは、強制振動と呼ばれています。(1)式で表される運動方程式の外力項がf=sin(2πft)のように、周期関数となります。ex408.mはex407.mに外力としてサイン関数を用い、引数に周波数fも加えたものです。外力の周波数f=1(Hz)、m=1(kg)、k=10(N/m)、c=1(Ns/m)、初期条件は静止状態として、t=0〜20(s)での変位を解いたものが、図6です。
図6を見ると、最初は系の固有振動周波数0.5[Hz]で振動しますが、次第に外力の周波数1[Hz]に移行することが分かります。このように、強制振動では、振動の周波数は外力の周波数に支配されます。
ex408.m
function ex408(f,m,c,k)
dydt=@(t,y) [y(2);(sin(2*pi*f*t)-c*y(2)-k*y(1))/m];
[t,y]=ode45(dydt,[0,20],[0;0]);
plot(t,y(:,1));grid('on');
title(['f=',num2str(f),' m=',num2str(m),' c=',num2str(c),' k=',num2str(k)]);
ylabel('Displacement[m]');
振動対策
振動対策は、バネ定数kや減衰係数cを変えることで、振動を減少させることです。ex408.mに各種の数値を入れて変位を確認する、といった方法も考えられますが、やみくもに試しても効率は良くありません。
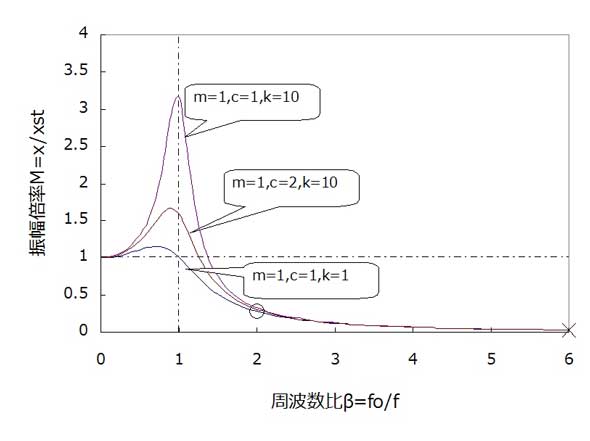
振動対策では、下記で表される振幅倍率の式を用いて検討します。振幅倍率Mfは変位の振幅xと静荷重での変位xstとの比で表されます。振幅倍率Mfは、加振源の周波数foと固有周波数fとの比βにより変化し、図7の曲線を描きます。
図6の振動ではm=1,c=1,k=10で、固有周波数は0.5(Hz)のため、周波数比は1/0.5=2となり、図の○印が振幅倍率となります。周波数比が1だと振幅倍率が最大となり、共振状態と呼ばれます。
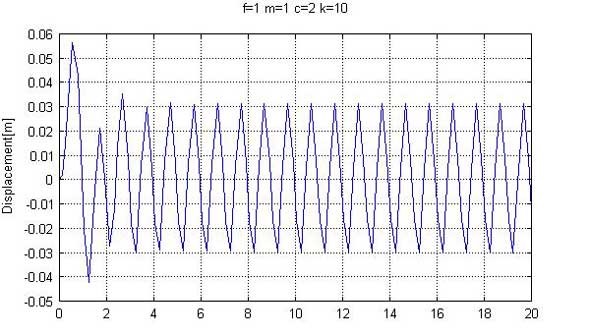
さて、減衰係数c=2とした曲線は○の位置では、ほぼ重なるため、減衰係数を大きくしても、振動低減には効果がないと考えられます。ex408.mでc=2として計算してみた結果が図8です。
振幅は0.03と図6とほぼ同じであり、効果が見られないことが分かります。
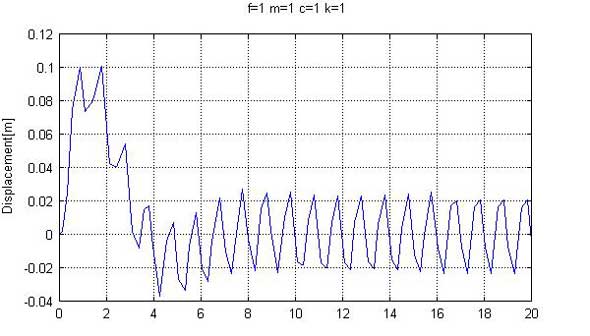
振動を低減させる方法として、図7から考えられることは、周波数比を大きくすることです。例えば、バネ定数を10分の1にして、k=1とすれば、固有周波数はf=1/2π=0.16(Hz)となり、周波数比β=1/0.16=6となり、図7の×印の位置になります。振幅倍率も小さくなっているため、振動低減に効果があると考えられます。そこで、ex408.mでk=1として、計算してみると、図9に示すように、振幅は0.02となり、振動低減に効果があると考えられます。
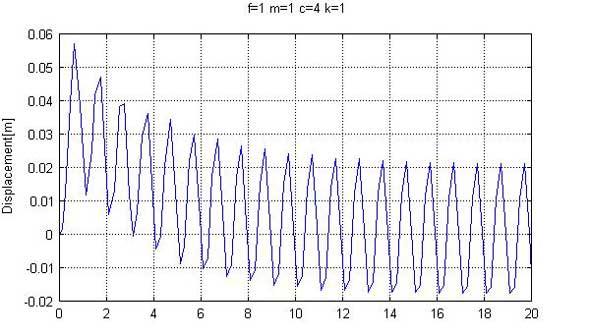
ただし、バネ定数を小さくしたため、始動時に大きく変位しています。そこで、減衰係数を大きくして、始動時の変化を抑えたのが図10です。
図10では、定常時の変位振幅が3分の2になり、始動時の過渡的な変位も同等となっています。
現実の回転機械では、質量以外のバネ定数や減衰係数は正確には分からないため、機械停止時の振動を測定し、「減衰速度」の項で説明した方法を用いて、バネ定数や減衰係数を予測します。その後、(2)式で振動対策を検討し、ex408.mのように、モデル式を数値的に解くことで、効果の確認と過渡的な影響を検討します。
シミュレーション編は今回で終了です。次回からは、制御工学編として、伝達関数やブロック線図、制御の安定性といったことについて、FreeMatを利用して説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフトでも、かなり高度な計算ができる! 今回はインストール編。工学計算の初心者もぜひチャレンジしよう。