振動問題をFreeMatで解いてみよう（その1）：無償ソフトで技術計算しよう【シミュレーション応用編】（2）（3/3 ページ）

今回は振り子の運動方程式や減衰振動を無償ソフト「FreeMat」で解いてみる。

[伊藤孝宏，MONOist]

減衰振動

　実際の振り子では、次第に振れが小さくなり、放っておくと静止します。これは、振り子の中心部分に摩擦力が働くためです（簡単のために、空気抵抗の影響は無視します）。摩擦力は速度に比例するため、（4）式に、摩擦力をη＊φとして追加します。

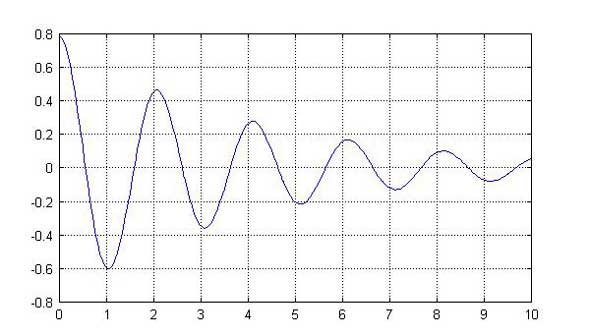
　数値解法では、ex405.mの1行目で、例えばη=0.5として、-0.5*th(2)を追加します。計算結果は図5に示すように、振幅が次第に減少する曲線となります。

dydt=@(t,th) [th(2);-0.5*th(2)-9.8*sin(th(1))];
ts=[0,10];n=20;
tspan=linspace(ts(1),ts(2),n);
t0=[pi/4;0];
tt=[];theta=[];
for k=1:n-1
    [t,th]=ode45(dydt,[tspan(k),tspan(k+1)],t0);
    t0=th(length(th),:);
    if(k<n-1)
        t(length(t))=[];th(length(th),:)=[];
    end
    tt=[tt,t];
    theta=[theta;th];
end
plot(tt,theta(:,1));grid('on');

ex406.m

＞＞「ex406.m」ダウンロード

図5：減衰振動の数値解法結果

　ηを負にすると、振動は増幅していきます。

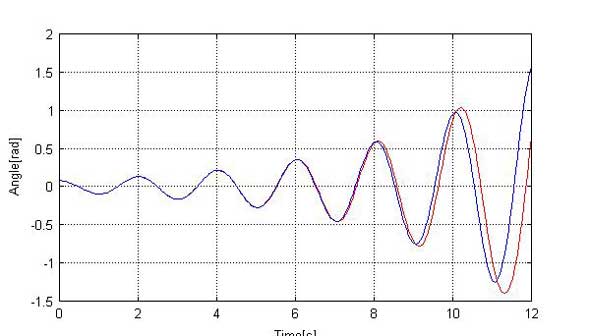
　ex406.mで、dydt=@(t,th) [th(2);0.5*th(2)-9.8*sin(th(1))];とすると、振動の増幅とともに、周期が長くなる様子が見られます。これが、振り子の等時性の破れで、dydt=@(t,th) [th(2);0.5*th(2)-9.8* th(1)];として計算した結果と比較した図6を見ると、その差が分かります。

図6：振り子の等時性の破れ

　図6で、青い線が0.5*th(2)-9.8* th(1)とした場合の結果で、振り子の周期は振幅には依存しません。一方、赤い線が0.5*th(2)-9.8*sin(th(1))とした場合の結果で、振り子の周期が振幅の増加とともに長くなっていることが分かります。

---

　次回は、機械振動のモデルであるバネ・マス・ダンパ系の振動について説明します。

参考文献

• 「MATLABハンドブック」小林一行著、秀和システム刊
• 「はじめてのFreeMat」赤間世紀著、工学社刊

無償ソフトで技術計算しよう

無償ソフトで技術計算しよう

無償の工学計算ソフトでも、かなり高度な計算ができる！

筆者紹介

伊藤孝宏（いとう・たかひろ）

1960年生。小型モーターメーカーのエンジニア。博士（工学）。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。