再帰アルゴリズムで「ハノイの塔」のプログラムを書く：無償ソフトで技術計算しよう【プログラミング処理編】（3）（2/2 ページ）

「再帰」とは、「自分で自分を呼び出す」ようなアルゴリズム。再帰アルゴリズムを使うと、有名なパズル「ハノイの塔」のプログラムがシンプルに書ける。

[伊藤孝宏，MONOist] PC用表示関連情報

LINE

Hatena

再帰グラフィックスによるコッホ曲線

　再帰アルゴリズムをグラフィックスに利用した例として、「コッホ曲線」を描画する方法を紹介します。コッホ曲線とは、数学者ヘルゲ・フォン・コッホが考案した曲線で、線分を3等分して、中央の線分を辺とする正三角形を作成するといった操作をそれぞれの辺に繰り返すことによって得られる図形です。

コッホ曲線（Wikipedia）

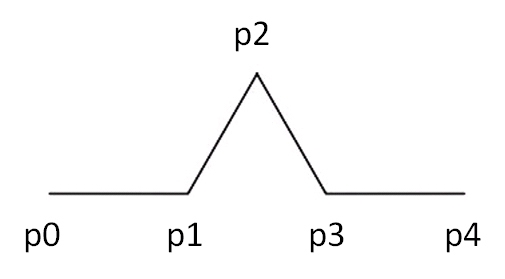
　図4を基に説明すると、線分p0-p4を三等分し、p1-p3を辺とする正三角形を作成すると、頂点p2が得られます。次に、点p0からp4を順に結ぶと、1次のコッホ曲線が得られます。この操作を各辺に行うと、2次のコッホ曲線が得られます。同様の操作を繰り返すと、高次のコッホ曲線が得られます。

図4　1次のコッホ曲線

　コッホ曲線を作成する関数mファイルを作成していきます。まず、図4の定義に基づいて、点p0、p1、p2、p3、p4の位置を計算します。ここでは、複素平面を利用することで1つの変数で処理することにします（複素平面とは、複素数の実数部がx座標、虚数部がy座標となる平面のこと）。

　P1はp0に(p4-p0)/3を加えたものになります。また、p3はp0に2*(p4-p0)/3を加えたものになります。P2は、長さがp1と同じで、水平から60度回転した向きの線分の先端になるので、p2=p1+(p1-p0)*exp(i*pi/3)となります。以上の4点を配列として並べると、1次のコッホ曲線になります。

　高次のコッホ曲線は、以上の操作をそれぞれの辺に繰り返せばよいので、先の操作を「koch(po,p4,n).m」という関数mファイルに定義し、[koch(po,p1,n-1), koch(p1,p2,n-1), koch(p2,p3,n-1), koch(p3,p4,n-1)]とすると、高次のコッホ曲線の配列が得られます。nは次数で、nが1ずつ減少し、0となった時点で、p0-p4を線分とする0次のコッホ曲線を出力して終了します。以上が下記の「koch.m」ファイルです。

function ret=koch(p0,p4,n)
if n==0
ret=[p0,p4];
else
p1=p0+1/3*(p4-p0);
p2=p1+(p1-p0)*exp(i*pi/3);
p3=p0+2/3*(p4-p0);
ret=[koch(p0,p1,n-1),koch(p1,p2,n-1),koch(p2,p3,n-1),koch(p3,p4,n-1)];
end

koch.m

＞＞「koch.m」ダウンロード

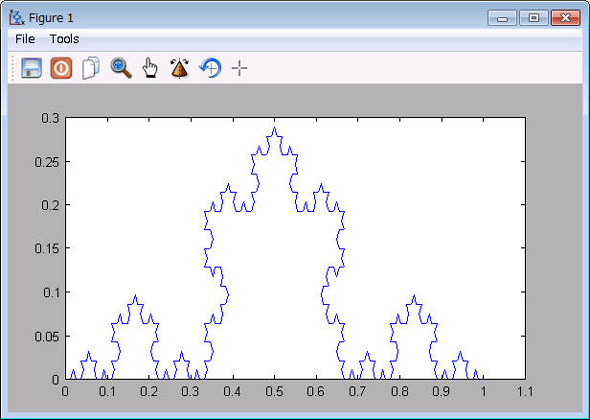
　コマンドウィンドウ上で以下のように入力すると、図5に示す4次のコッホ曲線が得られます。

--> plot(koch(0,1,4))

図5　4次のコッホ曲線

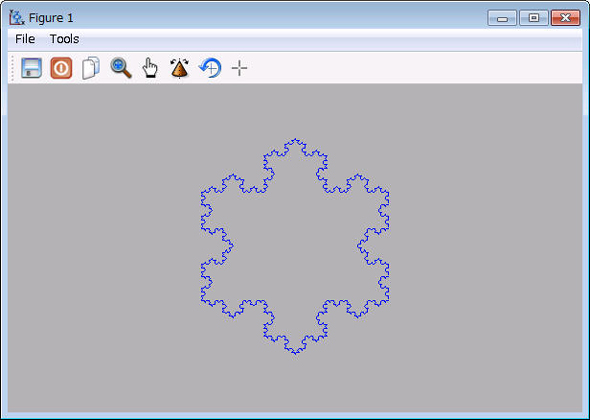
　コッホ曲線を利用して、雪の結晶のような図形を作成してみます。先ほどのコッホ曲線を120度回転させて、前の曲線の最後に接続するということを繰り返すと、図6に示すようなコッホ雪片あるいはコッホ島と呼ばれる図形が得られます。以下に示す「kochcurve.m」をワーキングフォルダに保存し、コマンドウィンドウでkochcurveと入力すると得られます。kochcurve.mでは、axis('equal');axis('off')として、縦横が等倍で、縦軸と横軸が非表示となるようにしています。

function kochcurve
ret1=koch(0,1,4);
ret2=ret1(end)+abs(ret1).*exp(i*(angle(ret1)-2/3*pi));
ret3=ret2(end)+abs(ret1).*exp(i*(angle(ret1)+2/3*pi));
ret=[ret1,ret2,ret3];
plot(ret);axis('equal');axis('off');
function ret=koch(p0,p4,n)
if n==0
ret=[p0,p4];
else
p1=p0+1/3*(p4-p0);
p2=p1+(p1-p0)*exp(i*pi/3);
p3=p0+2/3*(p4-p0);
ret=[koch(p0,p1,n-1),koch(p1,p2,n-1),koch(p2,p3,n-1),koch(p3,p4,n-1)];
end

kochcurve.m

＞＞「kochcurve.m」ダウンロード