タイヤは車体よりも先に最適化設計を採用――ブリヂストン事例など：MONOistゼミ 2014 レポート（3/3 ページ）

MONOist主催 CAEカレッジ「事例から学ぶ！ 設計者CAEの最前線」では、工学院大学 中島幸雄教授がブリヂストンにおけるタイヤの最適化設計事例について、サイバネットシステムの古市洋也氏が流体解析ツールと最適化ツールを使った小型軸流ファンの形状の最適化事例について紹介した。

[加藤まどみ，MONOist]

複合領域に関する2通りの最適化を紹介

　古市氏はこれらの分析を踏まえた上で2通りの最適化を示した。1つは単一目的最適化といって、目的関数を1つだけ設定することだ。目的関数は流量係数で、目標はその最大化となる。これは先ほどの流体解析のみによる最適化と設定はほぼ同じである。構造解析の結果は制約条件として利用する。今回は最大応力は初期設定値の2倍以下という条件を設定している。

　もう1つは多目的最適化といい、目的関数を2つ設定した。すなわち流体解析による流量係数の最大化および構造解析による最大応力の最小化である。多目的最適化は、目的関数同士がトレードオフの関係になることがある。その場合は最適解は1つにはならず、パレート解と呼ばれる複数の解を算出する。設計者はその複数のパレート解の中からバランスを調べながら適切と思われる解を設計案として採用することになる。

　単一目的最適化においては、2次多項式、RBFの応答曲面モデルを利用した最適化を実施した。単峰性の解空間のため、従来一般的に使われる「逐次2次計画法」（NLPQL）を使用した。最適解のみシミュレーションによって確認計算を実施し、最大応力が8万以下の制約条件で最適解を算出した（図8）。その結果、流量係数は初期設計値と比べて約41％改善した。

図8 最適解の算出

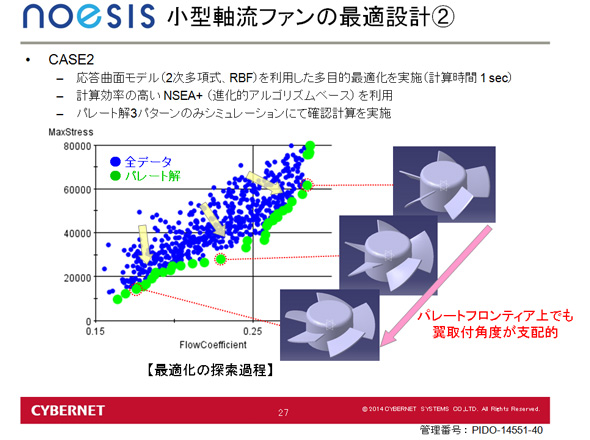
　多目的最適化では、同様の応答曲面モデルを利用し、計算効率の高い遺伝的アルゴリズムをベースに進化させたアルゴリズムのNSEA+を利用した。図9のグラフにある点のうち右寄りの緑の点が最終的に採用されたパレート解である。

図9 パレート解

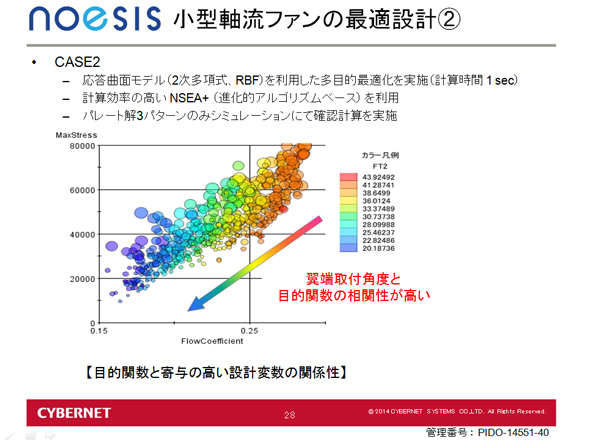
　これは、これ以上解の改善方向である右下に解がないという状態である。設計者はこれらの点のそれぞれのゲージを確認しながら、どの点を選ぶか検討することになる。なおバブルプロットも見ることが可能だ。図10は一番強度が大きかった先端取り付け角度をバブルプロットで表しており、色によって角度の傾向がつかめる。

図10 バブルプロット

　古市氏は最適化ツールのメリットについて、「作業を自動化することにより、工数の削減が期待されます。手作業の場合、夜間は中断することを考えると、半分の日数に削減できます。また設計者が付きっきりで入力などをしなくてよくなるというメリットもあります」と述べた。

Profile

加藤まどみ（かとう まどみ）

技術系ライター。出版社で製造業全般の取材・編集に携わったのちフリーとして活動。製造系CAD、CAE、CGツールの活用を中心に執筆する。