演算子と関数を駆使して統計的な計算をグラフプロットする:無償ソフトで技術計算しよう【入門編】(3)(2/2 ページ)
今回は、FreeMatの演算子と関数について説明する。また中心極限定理の実験でグラフをプロットしてみる。
例題:中心極限定理のプロット
さて、例題として、今回は中心極限定理の実験を行ってみます。中心極限定理とは、「平均μ、標準偏差σの母集団から、標本数nの標本を抽出して平均を求める。こうして求めたそれぞれの標本の平均は、母集団の分布とは関係なく、平均μで標準偏差が『σ/√n』の正規分布に近づく」というもので、統計学の基礎となるものです。簡単に言うと、「標本を多く集めれば集めるほど、より確かな推測ができるだろう」ということの根拠となるものです。
以上をFreeMatで実験してみましょう。
まず、母集団として、100行100列の0〜100に一様分布する乱数を用意します。0〜100に均等に分布するため平均μは50です。この母集団から100行10列を取り出して、行ごとの平均を求めます。こうすると、100個のデータが得られるので、この平均と標準偏差を計算し、ヒストグラムを作成します。同様にして、100行50列、100行100列でも行ごとの平均を求め、得られた100個のデータの平均と標準偏差を求めます。
以上の計算を行うプログラムが以下のファイル「ex02.m」です。
clear;
x=randi(zeros(100,100),100*ones(100,100));
n=[10,50,100];
for ii=1:3
xx=x(:,1:n(ii));
xmean=mean(xx,2);
figure(ii);
hist(xmean);
title(['n= ',num2str(n(ii)),' :mean= ',num2str(mean(xmean))...
' :Standard Deviation= ',num2str(std(xmean))]);
xlim([0,100]);
end
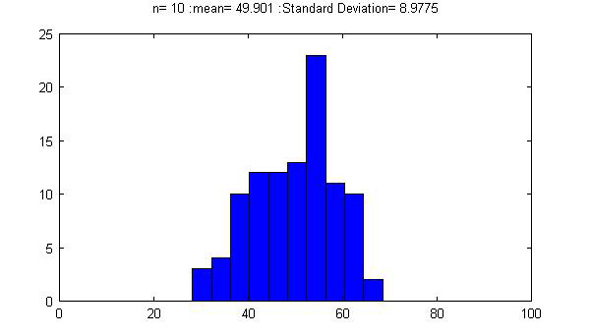
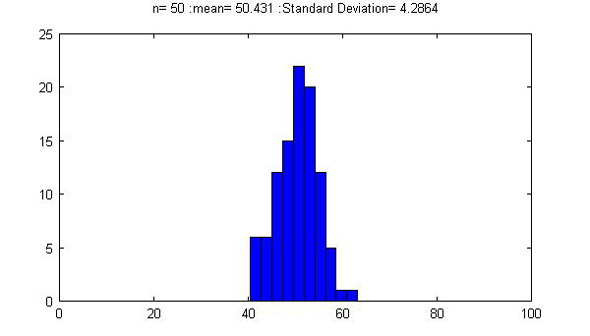
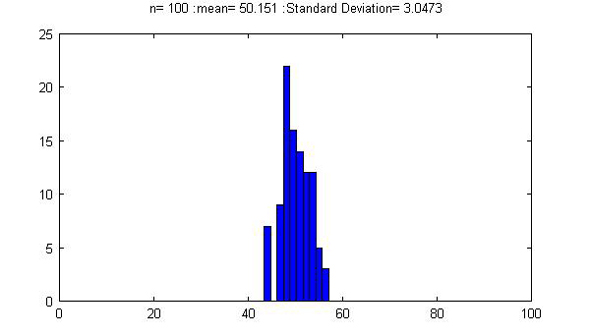
グラフにプロットされた結果は図1〜3です。
図1のサンプル数10では標準偏差は約9です。正規分布では-3σから3σの範囲に、ほとんどのデータが含まれるので(全体の99.7%)、この場合、50±27=23~77となります。つまり、サンプル数が10で1回実験を行い、平均を求めると、最悪の場合、23とか77という結果になります。
これに対して、図2の「サンプル数50」では標準偏差は「約4」で、結果は「50±12=38~62」となります。また、図3の「サンプル数100」では標準偏差は「約3」で、同様に「41~59」となります。ヒストグラムを見ても、サンプル数が多くなるほど、データのばらつきが小さくなることが分かります。
今回の実験では、母集団の分布には一様乱数を用いていますが、一般に、母集団の分布は正規分布に近い形状となることが多く、データのばらつきはもっと小さくなります。
いずれにしても、サンプル数が多くなればなるほど、より確からしい結果になることが実感できるかと思います。
詳細を説明すると、2行目で100行100列の乱数を発生させ、変数xに代入しています。
randiは整数の乱数を発生させる関数で、カッコ内は最小値の配列、最大値の配列です。例えば、randi([0,0;0,0],[100,100;100,100])とすると、0以上100以下の乱数を2行2列で発生させます。
100行100列では[ ]で直接記載することは不可能なので、最小の配列としてzeros(100,100)を用います。zeros(m,n)はm行n列の要素が全て0の配列を生成します。最大の配列は100*ones(100,100)とします。ones(m,n)はm行n列の要素が全て1の配列を生成します。
次に、xx=x(:,1:10)として、行数はそのままで、1〜10列目まで取り出して、変数xxとします。mean(xx,2)は平均を求める関数ですが、( )内2番目の数値が1の場合、縦方向に平均を求め、2番目の数値が2の場合は横方向に平均を求めます。
こうして求めた100個の平均をxmeanとして、hist(xmean)でヒストグラムを描きます。
以上の操作をサンプル数50と100でも行わせるため、サンプル数の配列「n=[10,50,100]」を用意し、forループでサンプル数配列の1番目、2番目、3番目と順にサンプル数としてn(ii)で与えます。図が上書きされるといけないので、figure(ii)で新たな図を出力させます。figureはグラフィックスを用意する関数で、figure(順番)とします。1枚しか図がない場合は不要です。
title関数はグラフにタイトルを記載する関数で、( )内にシングルクォーテーション「'」で文字を挟みます。例えば、title('n=')とするとグラフにn=というタイトルが記載されます。サンプル数もタイトルに入れるには数値を文字に変換しなければなりません。そこで、「num2str」関数を用いて文字列に変換します。文字列は文字の配列なので、[ ]内に , でつないでいけばタイトルに入れる文字列が完成します。つまり、title(['n=',um2str(10)])とすると、グラフに「n=10」というタイトルが記載されます。
xlim([0,100])で、3枚のヒストグラムが同じ幅になるようにx座標を「0〜100」に設定します。
先ほどのex02.mファイルをカレントディレクトリに保存して、「ex02」とするか、エディタで開いて実行させると、ヒストグラムを出力してくれます。ヒストグラムは3枚重なって表示されるので、1枚しか見えない場合でも、マウスでドラッグすると下にヒストグラムが現れます。なおプログラミングについては、本連載完結後に予定の「プログラミング編」で詳細に説明します。
◇
次回は配列について説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.