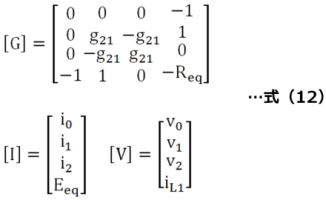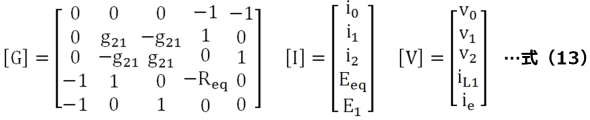SPICEの過渡解析（その2）：インダクタンス素子の場合：SPICEの仕組みとその活用設計（5）（4/4 ページ）

SPICEの過渡解析では、第4回で紹介したキャパシタンス素子の他に、インダクタンス素子も対象となる。第5回では、このインダクタンス素子を用いた回路の過渡解析について取り上げる。また、理想電圧源の組み込みについても説明する。

[加藤博二（Sifoen），MONOist]

理想電圧源によるLR回路の確認

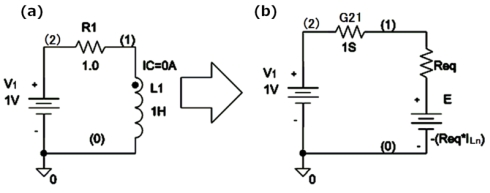
　今までは、内部抵抗のある電圧源として、コンダクタンスと電流源の組み合わせで電圧源を表現してきました。今回の記事の応用として、ここまで説明した理想電圧源を組み込んで図2（a）のLR回路を解析してみましょう。対象回路とその等価回路を図5に示します。

図5　（a）LR回路と節点番号（b）等価回路（クリックで拡大）

　ここでは理想電圧源V₁の電圧値をE₁、電流をI_eとします。それでは順を追って進めていきます。

（1）節点番号は0、1、2の3点で、節点2〜1間にコンダクタンスG₂₁が接続されています。従って、基準となる回路要素行列［G］、電流ベクトル［I］、電圧ベクトル［V］は式（11）のようになります。

（2）インダクタL₁を節点1〜0間に追加するため、行列［G］を拡張します。この結果、行列［G］、ベクトル［I］、［V］は式（12）の通り、4要素構成になります。行列［G］の拡張された要素はインダクタの組み込みの定式化に従って、（1,3）＝1、（0,3）=−1、（3,1）＝1、（3,0）＝−1、（3,3）＝−R_eqになります。

（3）理想電圧源V₁を節点2〜0間に追加するため、式（12）の行列［G］、ベクトル［I］、［V］を再び拡張します。この結果、行列［G］、ベクトル［I］、［V］は式（13）の通り5要素構成になります。

（4）式（13）から0行0列の要素を抜いて4×4の行列に縮小し、具体値を代入したものが式（14）です。g₂₁＝1（S）、R_eq＝10ですから実際の値は次のようになります。

　一方、電流ベクトル［I］の成分は、i₁＝i₂＝0、E_eq＝−R_eq×I_L0＝−10×0＝0（V）、E₁＝1（V）になります。

　式（14）の逆行列［G］⁻¹を求めて、電流ベクトル［I］に左からかければ電圧ベクトル［V］を求めることができます（［V］＝［G］⁻¹［I］）。

　それぞれの行列やベクトルは式（15）で表されますので、v₁＝0.909（V）、v₂＝1（V）、i_L1＝0.0909（A）、i_e＝−0.0909（A）となり、式（8）の結果と同じ値を得ることができます。

---

　次回からは、過渡解析で多くの解析技術者を悩ませる「収束エラー」について、主な要因と基本的な対処の手法を数回に分けて説明します。

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。