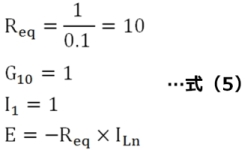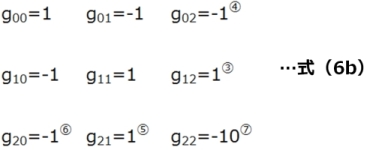SPICEの過渡解析（その2）：インダクタンス素子の場合：SPICEの仕組みとその活用設計（5）（2/4 ページ）

SPICEの過渡解析では、第4回で紹介したキャパシタンス素子の他に、インダクタンス素子も対象となる。第5回では、このインダクタンス素子を用いた回路の過渡解析について取り上げる。また、理想電圧源の組み込みについても説明する。

[加藤博二（Sifoen），MONOist]

過渡現象解析事例

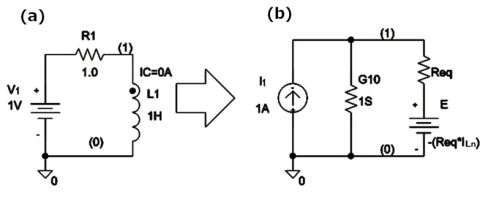
　実際の解析事例として図2（a）のLR回路を取り上げ、時刻0において電源V₁が接続された時の各部の電圧、電流の変化の様子を求めます。

• 条件1：初期条件としてインダクタL₁の電流は0Aとします
• 条件2：解析の時間ステップは0.1秒間隔で1秒間の解析を行います

図2　LR回路（クリックで拡大）

　等価回路は図2（b）に示すようになります。

• V₁とR₁（1Ω）⇒I₁とG₁₀
• L₁（1H）⇒R_eqとE
• 時間刻み⇒0.1秒

　これらを上記の定式化のルールに従って回路要素行列［G］を組み立てると各要素の定数は次のようになります。

　従って、回路要素行列［G］は、本来の節点番号0,1からなる2行2列を拡張した式（6a）の3行3列の行列になります。

　ここで、具体値を代入すると式（6b）のように値を決めることができます（式（6b）内の丸数字は定式化の手順番号です）。

　ここから0行と0列に関する要素を抜くと、解くべき回路要素行列［G］は、

となります。

　そして、電流ベクトル［I］は、

となります。

　初期値としてI_L0＝0を与えると、E＝−R_eq×I_L0＝0ですので、電流ベクトルの具体値は

となります。つまり、この行列を解けば式（8）のように各値を得ることができます。

　この値は、初回刻み時間Δtが経過したときの各節点値です（この例では0.1秒後）。このようにして新しい節点1の電圧v₁、インダクタ電流i_L1が求まりましたので、式（5）のインダクタ等価電圧E（＝−R_eq×I_Ln）を更新して電流ベクトル［I］を組み直し、上記と同様に解けば計算を進めることができます。

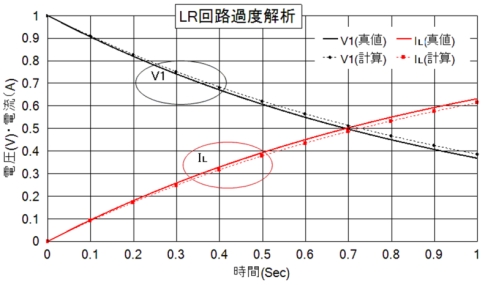
　この繰り返しの結果を図3に示すとともに、参考として代数学的な真値も併記します。1次近似でかつ、粗い刻み時間ですので真値とは差を生じていますが、現象そのものは再現できています。

図3　LR回路応答波形（クリックで拡大）