ヒントは「引っ繰り返す」! 難しくない板金設計ワザ:甚さんの「バンバン板金設計でキャリアアップ」(13)(2/3 ページ)
あれ? どこかで見たことがある箱だけど? ――いやいや、新しいお題です。レゴブロック箱から板金箱にできるかな? 今まで紹介した設計ワザを組み合わせて考えてみよう。
あの、もうちょっと考える時間を……。
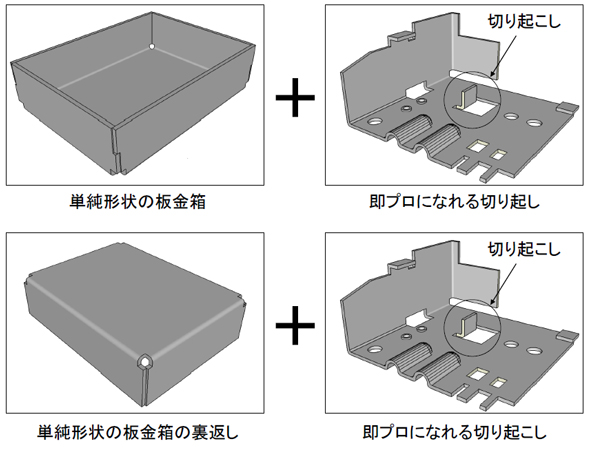
私はもう考えてきました! これでいかがでしょうか?(図3)
すんばらしいじゃねぇかい、エリカちゃん! どうやって、頭の中のイメージ(レゴブロックの絵)を具現化したのか、ちょいと教えてくんねぇかい?
分かりました。まず、前回の甚さんのアドバイスを応用しました。「設計とは組み合わせの技術」に尽きます。今回は新しい発想は避けてみました(図4)。
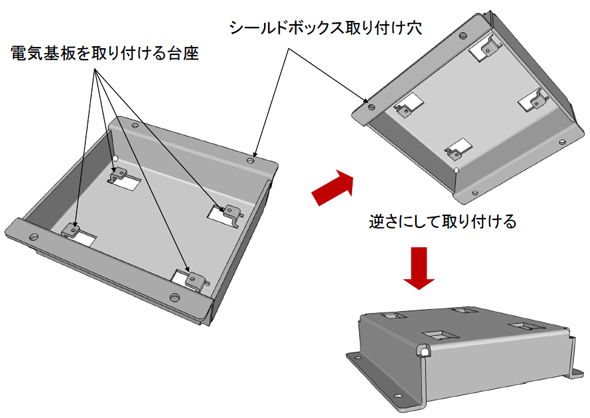
図4の上側は、第11回で紹介した「組み合わせの技術」です。その下側が、今回のエリカちゃんのアイデアです。板金箱を裏返しています。
うわぁ〜! エリカちゃんってすごい! さすが、専門学校卒だね。僕も専門学校へ行けばよかったなぁ……。シュン……。
いんや〜! ますます、すんばらしいじゃねぇかい、エリカちゃん! しかし、ちょいと残念なところが一カ所ある。良君、エリカちゃんの図面を検図しろ。これは命令だが、ま、いつもやってんだろ?
え〜〜とぉ、……え〜〜とぉ。
ドキドキ……。
さっさと言いやがれ!
え〜〜とぉ……ワカンナイ! 残念ナトコロッテドレカナァ? テヘペロー。
うわっ、イラッとしました!
オメェは、いつからローラになったんだぁ、あん!?
じょ、ジョークですよ! 緊張した場を和ますための!
和ませなくていい!! いつまで待っても答えはで出ねぇだろうだから、図5を見ろ!! さっさとな!
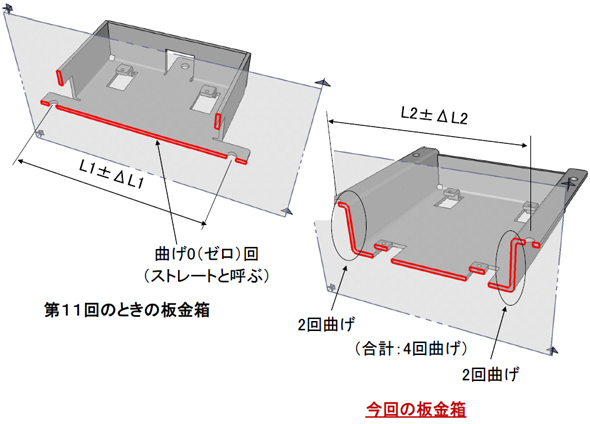
図5における取り付け穴の称呼寸法は、「L1=L2=300mm」とします。
まず、図5の左側、つまり第11回で紹介した板金箱の取り付け穴に注目してください。
「L1±ΔL1=300±0.22」となります。図示せぬ取り付けねじをM4とした場合、図5にある左右に2個ずつある取り付け穴は「φ5」で十分でしょう。
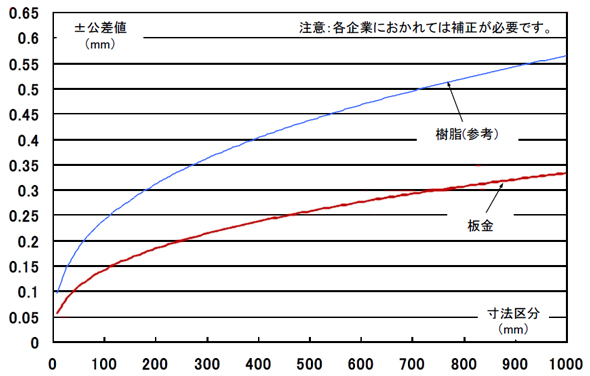
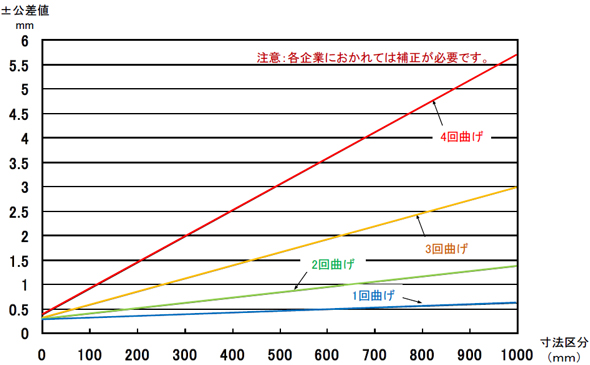
ここで、前述の「±0.22」は、図6で求めました。
どおお! 何、ナニ、これっ! 大学や大学院では見なかったデータですぞ〜。もう、ショック……。
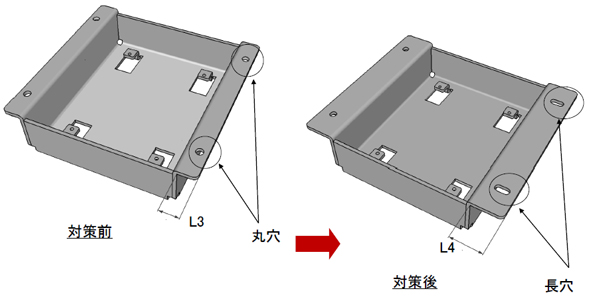
次に、図5の右側、つまり、今回の板金箱の取り付け穴に注目します。
「L2±ΔL2=300±2」となります。なんと、公差の「±2」は、前述の9倍です。図示せぬ取り付けねじをM4とした場合、図5における左右2つずつの取り付け穴はφ5では不十分です。図7のように片側を丸穴から長穴に変更する必要があります。
「L2±ΔL2=300±2」の「±2」は、図8の「4回曲げ」で求めました。
Copyright © ITmedia, Inc. All Rights Reserved.