自由度と、リンク機構の基本のいろいろ:メカメカリンクで設計しよう(1)(2/3 ページ)
今回は4節リンクのうち、2次元動作について解説する。「自由度」や「対偶」についてあらためて確認していく。
「自由度」って、何だろう?
私の技術士事務所の名称にも使っている「自由度」とは何でしょうか?
自由度とは、「数式モデルにおいて、ある物体を動かすことができる方向の数」と定義されます。しかし、言葉が難しすぎて全くイメージできないと思います。
自由度を簡単に説明すると、1本の軸の上で左右問わず回転だけ動作できる場合、「1つの自由度を持つ」といいます。また、1本の軸の上で回転できずに、前後にスライドする場合も「1つの自由度を持つ」といいます。
ここで、1本の軸の上で、回転とスライドの2つの動きができる場合を「2つの自由度を持つ」といい、動く方向や種類が増えるごとに自由度が増えていきます。
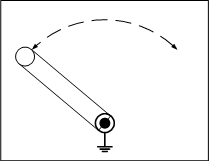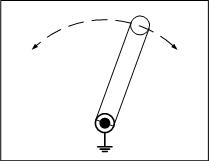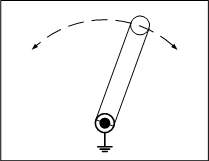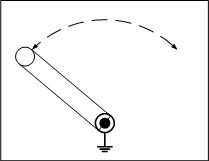
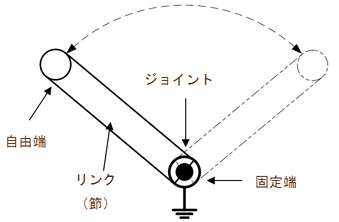
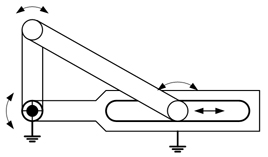
最も基本的な動作をするリンク機構を図1に示します。このリンク機構は、回転運動のみができることから、1自由度の特性を持つことが分かります。
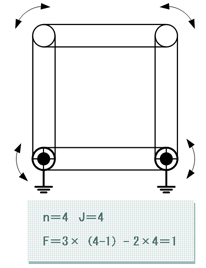
リンク機構の自由度の数は、グルーブラーの式から求めることができます。
- F=3(n-1)−2J
- F:自由度
- n:リンク(節)の総数(可動リンクに加えて固定地面部、スライド部を含む)
- J:ジョイントが持つ1自由度の総数
以下に、さまざまな構造の自由度を確認してみましょう。
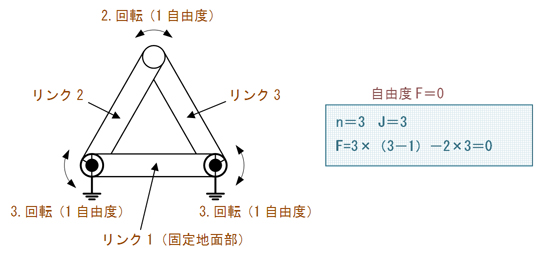
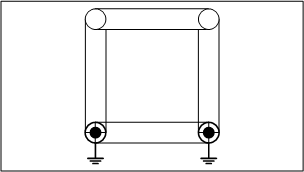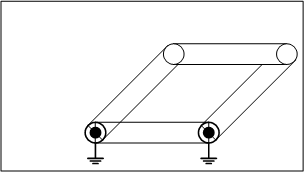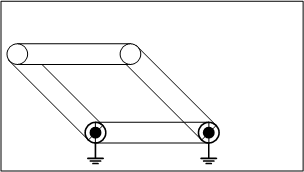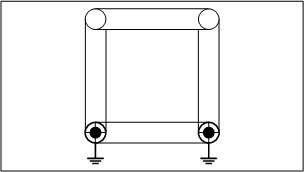
1.トラス構造
図2に示す三節リンクは自由度がゼロになり、機構として動かない、つまり、動作するリンク機構として使うものではなく、何かを保持するための構造物として利用することが分かります。これを「固定連鎖」と呼びます。
「トラス」とは、全てのジョイントが自由に回転できる回転対偶で構成した骨組み構造です。ジョイントは回転できますがモーメントが伝達されないため、圧縮応力や引っ張り応力のような内力が働くことで外力に抵抗します。「ラーメン」とは、ジョイントを溶接などによって回転できないよう構成した骨組み構造です。剛体となることで曲げモーメントに抵抗する作用によって外力に抵抗します。
2.四節リンク
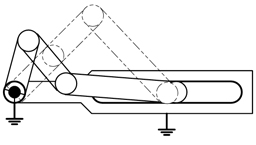
四節リンクは自由度が1になり、機構として、ある決まった動作を繰り返すことが分かります。
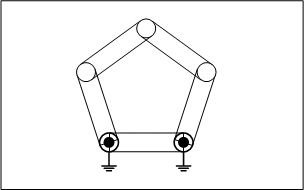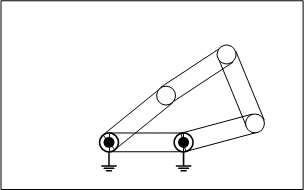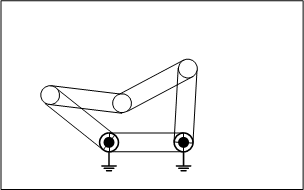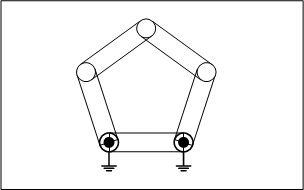
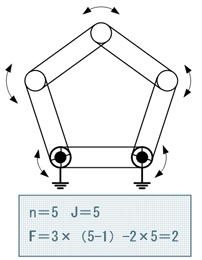
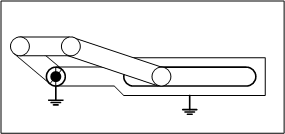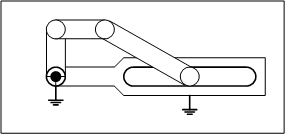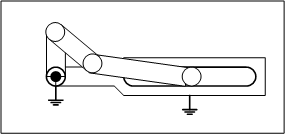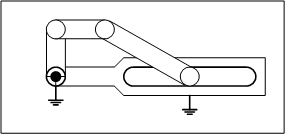
3.五節リンク
五節リンクは自由度が2になり、機構として、決まった動作に従わず、不定な動作をすることが分かります。これはリンク機構として、どんな動きになるのか想定できないため、動作の信頼性を保証しなければいけない機械装置に使うことはできません。
リンク機構には、回転するという特性に加えて、移動(スライド)するという特性を組み合わせることができます。
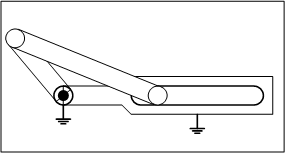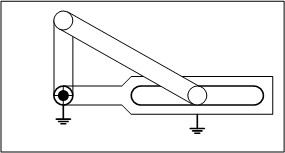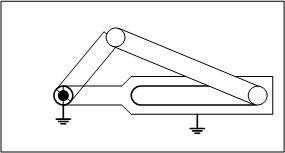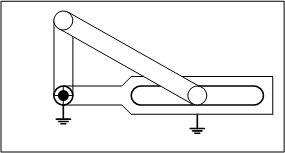
4.四節スライダクランク
四節スライダクランクは自由度が1になり、機構として、ある決まった動作を繰り返すことが分かります。
5.五節スライダクランク
五節スライダクランクは自由度が2になり、機構として、決まった動作に従わず、不定な動作をすることが分かります。これはリンク機構として、どんな動きになるのか想定できないため、動作の信頼性を保証しなければいけない機械装置に使うことはできません。
以上から、五節リンクのように、自由度が2以上になるとさまざまな動きができる半面、リンクの動きを制御できないことが分かりました。そのため、1つのモータで複数の節からなるリンク機構を動かすには、四節リンクが適しているのです。
Copyright © ITmedia, Inc. All Rights Reserved.