ブンさんの家宝じゃないよ、分散の加法性!:公差解析 基本中の基本(3)(3/4 ページ)
デイちゃんの部品の公差をもっと広げることはできるだろうか? 今回は、「分散の加法性」について愉快に分かりやすく解説!
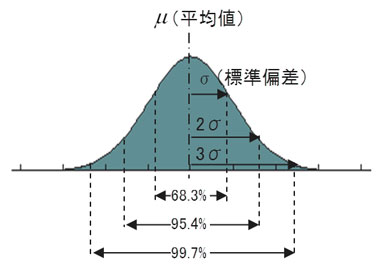
例えばこーんな分布がありました(図4)。この分布は『正規分布』っていってネ、たくさんのデータをサンプリングしたときに集計するとよく見られる、っていわれてる分布ナノYO。この正規分布とは、実は、いま計算した平均値(μ)と標準偏差(σ)で決まるカタチで、平均値から+σ、−σいったところに『変曲点』がアルの! オーケー?
μ:サンプルの平均値 σ:サンプルの標準偏差
正規分布はネ、μ±σの面積が全体の68.3%、μ±2σ(σの2倍)の面積が全体の95.4%、μ±3σ(σの3倍)の面積が全体の99.7%を占めているのよ。だからミーはさっき『3σ』っていったのネ! 3σは、『1000個作って3個が不良』。それを気にスル? それとも、シナーイ? ――というふうに目安にすることが多いのYO! ちなみに、この絵にはないけれど、4σは99.9%。つまり、どんどん不良の数が減っていくのね
で、『分散の加法性』は?
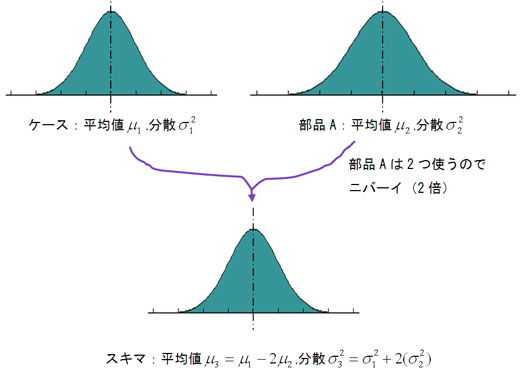
仮にケースの平均をμ1、分散をσ 12とするYO。そして、部品Aの平均をμ2、分散をσ22。小さな下付き数字を付けて、ケース(1)と部品A(2)って、区別してみたYO。
それぞれが正規分布でできていたとするデショ? このときにそれぞれからランダムに1個ずつ取り出して組み立ててスキマを測定したとシマース。
そうすると、
- スキマの平均は、μ1−2μ2 (ケースの平均値−部品Aの平均値の2倍)
- 分散はσ 12+2(σ 22) (ケースの分散+部品Aの分散の2倍)
という関係が成り立つの。これが『分散の加法性』ネ〜。部品Aは2つ使うから、2倍するのを忘れないでね。スキマは『ケースの寸法−部品Aの寸法』で計算できるから、今回のスキマの平均値は引き算で出したの。ダケド、もし足し算で計算する関係性だったら、その平均値は足し算で計算ネッ!
えーっと……。組み立てたときのスキマがどんなふうになるか、それぞれの部品の平均値と分散から予測できるっていうコトですか〜。この分散と公差ってどんな関係があるの?
ユー、いいところに気が付いたネ! 分散はサンプリングのバラツキをヒョーゲンしてるの。でも、公差とは違うの。公差は、標準偏差をモトに『±3σ』といった感じで設定されるコトもあったり、サンプリングデータの3σのバラツキを基に設定するコトもあったり、公差とバラツキはつかず離れずのカンケーなのよ。ユーたちとミーみたいにね。フフ……
はぁ? ……まーいいわ! それでっ?
じゃあ、もしも3σ以内でケースと部品Aが作れたとしたら、午前中に計算してみた結果は、3σ(99.7%)の確率の結果になるってことかぁ。それで結果がワーストケースよりも良くなったわけなんだね。分かりましたー
この前提で計算した場合、
±0.1658になるから、さらに四捨五入して、 ⇒±0.17だね。
スキマの寸法値に当てはめると、
10.15−(2×4.85)=0.45 ⇒ 0.45±0.17
だから、スキマの範囲は0.28〜0.62(mm)になったでしょ? でもスキマは0.2(mm)以上あればいいんだから、もうちょっと公差を広げても(0.08(mm)分、スキマを詰める方向に追い込める)大丈夫なんだよねっ!
ケースは購入品だから、部品Aで何とかしたいな。逆算してもいい? えーっと、計算結果は、0.45±0.17(mm)でした。でも、スキマを0.2(mm)に合わせ込むには、0.45±0.25(mm)(±0.08(mm)広げる)にしても大丈夫ってことでしょ? ……ってことは
おぉ! 部品Aの公差、もともと4.85±0.05(mm)だったのが、4.85±0.14(mm)に広がったぞ〜! これならいまの機械でも何とかなるよ! ありがとう、おじさん!
ノー! ミーは、小悪魔さん! でもユー、気を付けてネ。これは同じ製品をタップリ作ったときで、統計的なデータが取れるときの結果ヨ!
Copyright © ITmedia, Inc. All Rights Reserved.