ターボ機器の流体解析と最適化設計：実務経験者が教える！ ターボ機器の設計解析の勘所（6）（3/4 ページ）

最終回は、これまで説明してきた流体解析を利用したターボ機械の「最適化設計」について解説する

[山本幸広／ヴァイナス，＠IT MONOist]

■勾配法

　最適化を考えるうえで、最も代表的な方法が勾配法（参考文献［8］）です。目的関数が最大化を示す問題を取り扱うときは、応答曲面上を山の頂上に向かって登ってゆくので、「山登り法」ともいわれています。基本的な考え方はとても単純で、ある地点からスタートして山の頂上に着くためには、その場で一番勾配のきつい方向に登ってゆけばよい、というものです。

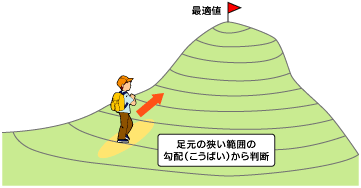
　ごく近傍の設計変数の範囲から勾配を求めることは、まるで真っ暗闇の中で懐中電灯を持つ登山者が、電灯で照らされるごく狭い範囲の斜面の状況を基に手探りで頂上を目指すような状態といえます。図6.4で示す絵をご覧いただくと、そのイメージが分かるのではないでしょうか。

図6.4　勾配（こうばい）法の考え方

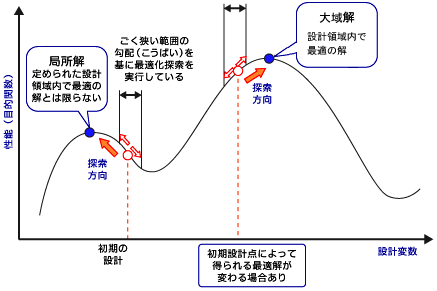
　このように手探りで頂上を目指す状態では、山全体の形は見えるはずがありません。勾配法による最適化では、対象となる範囲すべての中で最適な値を取るとは限りません。小さなピーク（極値）が途中に存在していると、全体の中での最適値ではなくても、その極値を最適値と認識してしまいます。つまり、最適化の始めに性能を求める設計点によって、得られる最適値が変わることになります。このように勾配法は、スタート地点に近い局所解を求める最適化手法、といえるでしょう。図6.5のような複数のピークが応答曲面に見られるような問題を多峰性、拘束領域内でピークが1つだけの場合は単峰性の問題といいます。流体設計問題は、複雑な多峰性の関係を持つケースがほとんどであると考えられます。

図6.5　局所解と大域解

■焼きなまし法（Simulated Annealing）

　焼きなまし法は、金属工学における焼きなましのプロセスからヒントを得たアルゴリズムです。焼きなましは、金属材料を熱して溶解状態にした後で徐々に冷やして、結晶を成長させて欠陥を減らす作業のことです。最初の加熱によって金属原子は初期の位置（内部エネルギーがローカルな極小状態）から離され、よりエネルギーの高い状態を推移します。そして、ゆっくりと冷却することによって、原子は焼きなましを行う前より内部エネルギーがさらに小さくなる可能性が高くなります。

　焼きなまし法では、探索する設計空間の各点は物理システムの状態に対応し、目的関数は物理状態の「内部エネルギー」に対応します。従って最適化目標は、「エネルギーを最小の状態にすること」となります。

　このような概念を導入することによって、確率的な揺らぎが導入されます。つまり勾配法が目的関数値を改善する方向にしか最適化を進めなかったのに対し、ある一定の制限下で改悪となる方向にも最適化が進むことを許容します。これで、局所最適解を通り過ぎる探索経路を取ることができますので、大域的な最適解に到達することができるわけです。それほどCFD計算の実行回数を重ねなくとも大域解を求められることは焼きなまし法の大きな長所といえるでしょう。

　一方、焼きなまし法により、有限の試行回数で、より早く近似的な最適解を得るには、探索の過程で設計変数を変化させるステップの幅（これを焼きなまし法では擾乱（じょうらん）といいます）の調整方法や、温度（確率）を徐々に下げていく冷却過程（クーリングスケジュール）の制御が重要なのですが、このチューニング方法は非常に経験的で、調整が難しいという課題もあります。このような問題に対しては、いくつかのチューニング方法が研究者から提案されています。

　また、焼きなまし法も目的関数が1つだけ選択できる、単目的最適化手法であるのは、勾配法と同じです。

■遺伝的アルゴリズム（Generic Algorithm）

　ダーウィンの進化論をモデルとした最適化アルゴリズムは、進化アルゴリズムと呼ばれます。つまり、すべての生物は、生殖・淘汰・突然変異によって、環境に適応しながら進化する、そのプロセスを応用しています。遺伝的アルゴリスム（参考文献［9］）は進化的アルゴリズムのうちの1つであり、その中では最もポピュラーな手法です。

　設計変数は「遺伝子」として対応付けられます。その「遺伝子」を持つ生物の個体がN個集まって集団を作ります。この集団の中で、環境に適用する度合い（適用度）を指標として優劣を決めます。このときの「適用度」が目的関数に当たります。このようにして最適化問題における設計変数と目的関数の関係を1個の生物に置き換えて、遺伝を繰り返すことによる「進化」を求めるわけです。実際のプロセスは次に示す手順で進められます。

1. 集団の中の個体間で、適用度を指標として優劣を決める（1〜N位まで並べる）
2. 一定の順位以下の個体は削除。一方、逆に一定の順位以内の個体はペアリング・交叉（こうさ）をせずに残す（エリート戦略）
3. 残った個体の間で、ランダムに2個ずつの個体を選んでペアリングする
4. ペアリングされた個体同士が交叉して、優秀な親の「遺伝子」を持った子供が産まれる。子供が生まれた結果、集団内の個体数はN個で保持される
5. 次の世代に移った状態で、（1）〜（4）を繰り返す
6. ある段階で個体中の「遺伝子」を強制的に操作して、「突然変異」を起こす
7. 終了条件が来るまで、（1）から（6）を繰り返す

　以上の手順を見ると、遺伝的アルゴリズムは、勾配法や焼きなまし法と比べると大きく異なる特徴を持っていることが分かります。勾配情報を用いず、目的関数値そのものを取り扱うことや、1つの解ではなく解の集団として最適化が進行していくというものです。このような特徴から、一般的に局所解に収束しにくく、大域的な最適解が得られること、つまり多峰性の問題にも強いこと、多目的最適化問題を取り扱い可能であること、また並列化に向いており、豊富な設備リソースがあれば大規模な問題を短時間で解けることが期待できるなど、さまざまな長所を持ちます。さらに勾配情報を用いないことから、目的関数が定式化しにくい問題であったり、最適化問題での性能が明確になっていなかったりする場合は、遺伝的アルゴリズムを使った最適化は効果的です。

　一方、確率論的なアプローチで、「良い答え」を迅速に導き出すことができますが、その答えが真に最適な値である保証はなく、現在得られている最適解に近い設計変数の組み合わせにおいて、より最適な解が見いだされる可能性はあります。