ターボ機器の流体解析と最適化設計:実務経験者が教える! ターボ機器の設計解析の勘所(6)(2/4 ページ)
最終回は、これまで説明してきた流体解析を利用したターボ機械の「最適化設計」について解説する
2-2 設計課題で与えられた変数の範囲で、パラメータスタディを行う(実験計画法)
続いて、ターボ機械の最適化設計において選択した設計変数(流路または羽根形状を規定する変数)と目的関数(性能値)の関係を求めます。ただしこの関係は、実際に流れ解析を実行して性能を求めなければ分かりません。設計変数を変更して、形状が少し変わったとき、性能にはどのような影響があるのかを確認するためには、複数の設計変数の下で流れ解析を実行して、傾向を求める必要があります。
ターボ機械の設計開発業務で最適化設計をする際には、業務の効率化が求められます。すなわち、できるだけ少ないCFD計算ケース数で、設計変数と性能値の関係を求めなければなりません。このような形で、実験試行を効率よく行うためにさまざまなサンプリング手法が考え出されています。「サンプリング」というのは、設計変数を連続的に変えるのではなく、離散的な(飛び飛びの)値を選び出して、流れ解析を実行することを意味します。
最適化設計の中で使われるサンプリング手法は、ほとんどが実験計画法に分類されます。実験計画法では、ある結果に対して、影響していると考えられる要因と、その要因がどのレベルにあるのかを示す水準を設定して、実験的に組み合せて変化させてデータを得る、という手順を取ります。
ターボ機械の羽根車に置き換えて考えると、表6.2のようになります。
このように、要因すべてに含まれる水準すべてを組み合わせて実行すると、膨大な回数のCFD計算が必要になります。そこで、「ラテン方格法」や「直交表」などによる実験計画を行います。これらの手法の詳細を述べると長くなりますので、文献を参照ください(参考文献[4])。
また、設計変数の数を増やすと、設計変数と目的関数の関係を精度よく求めるために必要なサンプル数(設計変数の組み合わせの数)も多く必要になります。ラテン方格の変数選択の偏りをなくした、最適ラテン方格実験計画では、目的関数が設計変数の2次式で近似されると仮定すると、
最低サンプル数=(n+1)(n+2)/2 nは設計変数の数
と表されます。
設計変数が5までの最適ラテン方格実験計画で必要なサンプル数は表6.3で示されるとおりです。
目的関数の形が分からない場合は、表6.3で示される最低サンプル数の1.5〜2倍のサンプル数を使用することが多いです。ちなみに、設計変数が3個以上のラテン方格実験計画を「ラテン超方格法」と呼んでいます。
2-3 設計変数と目的関数の関係を求める(応答曲面法)
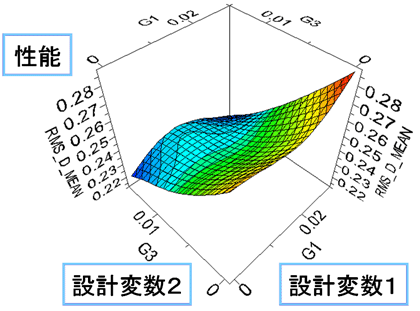
飛び飛びの設計変数値の組み合わせですが、設計変数と目的関数の関係が随分見えてきました。しかし、最適化設計を行って、最も優れた性能を求めるときには、できる限り真の最適値に近い設計変数の組み合わせを探し求めるために、サンプリングされていない設計変数の組み合わせにおいても性能を求める必要が出てきます。ここで、あらためてCFD計算を実行して性能を求めると、非常に膨大な時間がかかってしまいます。そこで、実験計画法で求めた離散的な設計変数と目的関数の関係を使って、数学的に近似したモデルを作ることにより連続的な関係を仮定し、この関係から任意の設計変数値の組み合わせにおける性能値を求めることを考えます。これを「応答曲面法」(または近似手法)(参考文献[5])と呼びます。応答曲面法で求められた近似モデルによって、CFD計算なしで、短い時間で何百回、何千回と試行して性能を求めることができます。
複数の設計変数の値の組み合わせで得られる場を「設計空間」と呼びます。現実空間は、横方向の距離(x)、奥行き方向の距離(y)、鉛直方向の距離(z)の3つの値を用いて位置を一意的に求めることができますが、これを設計変数に置き換えたものと考えてください。設計空間内では近似モデルで表現される目的関数(応答曲面)があり、例えば最大化目的を探索する場合は、応答曲面の最も高い場所を示す位置(設計点)が最適解を得る設計変数の組み合わせとなります。
この近似モデルも、さまざまな手法があります。離散化されている目的関数の分布を確認して、どの程度単純な曲面で表現できるかにより、使い分けます。単純なn次多項式による近似曲線やテイラー級数などの多項式近似、設計空間内の離散的な点から確率場の値を予測して目的関数の分布を求める「クリギング(kriging)法」、ニューラルネットワークを利用して設計点を補間する「RBF(Radial Basis Function)」などの手法があります。
近似モデルの妥当性は、サンプリングされた設計変数の組み合わせにおける目的関数と、近似モデル上の目的関数の間の重相関係数を用いて確認します。
重相関係数が0.90以上の値を示せば、近似モデルは傾向として妥当である、と見なします。妥当でないと判断された場合は、サンプル数を増やす、設計変数の範囲を狭める、といった対策が考えられます。
2-4 いよいよ最適値の探索
これで、設計変数と性能の関係が、連続的な領域で明らかになったので、その関係の下で最も優れた性能が得られる設計点を探索します。最適化問題を解くための探索手法はさまざまなものが提案されてきていますが、流体設計問題に適用される代表的な最適化手法として、「勾配(こうばい)法」「焼きなまし法」「遺伝的アルゴリズム」の3つについて、説明します。(参考文献[6][7])
Copyright © ITmedia, Inc. All Rights Reserved.