摩擦係数というより摩擦係数の変数だ：ピタゴラスイッチの計算書を作ろう（2）（3/4 ページ）

摩擦係数μは、斜面を滑りながら転がっているか、または滑らずに転がっているかにより意味が異なるって理解していた？

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

シミュレーションの活用

銀二「そういうことだね。サブ・システム1が設計できたところで、その計算問題を宿題として出すから、やっといてな。一見計算が面倒くさそうだけど、実は案外簡単だよ。ところで、実際はさらに複雑で、摩擦係数が大きいから必ず転がり落ちるとは限らない」

草太「えっ？ どういうこと」

銀二「スロープの形状によっては、ボールがスロープ面から離れる場合がある。図2.5を見れば分かるよね」

図2.5　ボールとスロープ面

草太「なるほど。スロープの形状変化が大きいと、そういう場合もあり得るね」

銀二「スロープの形状変化が大きいと、なぜボールがスロープ面から離れるんだい？｣

草太「経験上なんとなく……、誰でもそう思うんじゃないの？」

銀二「遠心力が働くからだよ」

図2.6　曲面上を動くボールに作用する

　スロープ形状の曲率半径をρとすると、スロープ形状に沿ってボールが動くとするとボールにはmv 2／ρの遠心力が働くから、形状変化が大きいところでは遠心力が大きくなって、ボールはスロープ面から浮いてしまいます（図2.6）。

　別のいい方をすれば、「形状変化の大きい場所では向心力がないと、スロープに沿ってボールは動かない」ということですね。

銀二「(2-6)から(2-13)までの計算で、スロープ面からボールが受ける力Ｎはmg・cosθとして計算したけど、本当は以下式のようになる」

銀二「こうなると手計算で対応するのは大変だ。ああ、非常に面倒くさいね。しかし面倒でも、もし本物の装置が数億も掛かるんであれば、私は絶対検討するけどね。もっとも、速度が小さくて、曲率が大きければ遠心力は無視できるから、形状によっては遠心力を0として計算していい場合がある。人間の直観力は鋭いから、目で見た判断が正しいことが結構ある。その場合でも本当は遠心力が作用しているってことを認識しておくことが重要だ」

　最近は、シミュレーション・ソフトの操作性が良くなって、複雑な計算でも誰もが簡単にできるようになりましたね。例えば前ページ図2.4のスロープ上を半径5.5mmのパチンコ玉を転がしたときのエネルギー損失が簡単に計算できます。

図2.7　摩擦係数とスロープ戻り高さ

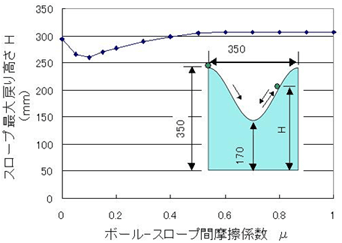
　図2.7は、パチンコ玉が図2.4のスロープを降って登るときの最大高さをシミュレーションで求めたものですが、摩擦係数が0.1のときが一番低いのが分かると思います。

　また図2.7から判断すると、摩擦係数が0.5以上となると戻りの高さはほとんど同じになります。

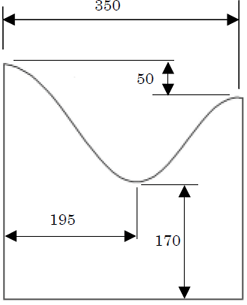
　　　段差＝50mm

とすればなんとか次のサブ・システムにボールをつなげることができそうです。

　よって、

• ボールの材質は摩擦係数の大きいゴム
• 段差は50mm以上とすべき

であることがはっきりします。

草太「ところで摩擦係数0でも、出発点と戻りの高さの差は50mm以上あるね。これはどういうこと？」

銀二「シミュレーションモデルのスロープは完全には曲線でなくて、折れ線近似で作られているから、折れ点を通過するときに微小な跳ね返りが発生しているんだね」

図2.8　スロープの折れ線

　跳ね返ったボールが斜面と衝突するときにスロープ面に垂直方向の速度エネルギーの損失が発生するので、摩擦係数が0でもシミュレーションでは完全には元の位置まで戻ってきません。

　摩擦係数が大きいときは、エネルギーがボールの回転に費やされるため、ボールの移動速度は遅くなります。だから、折れ線（図2.8）を通過するときの速度エネルギー損失も少ないのです。

銀二「ともかく、重要なことはシミュレーションによって“摩擦係数が0.1付近のボールは設計課題のピタゴラスイッチには向かない”ってことが分かったってことだ」

草太「うん。これでようやくスロープの設計ができたわけだね。さっそく100円ショップへ行って、スーパーボールやビー玉を買ってきて、段差を50mmにして作ってやってみるよ」

銀二「スロープはどうする？｣

草太「フレキシブルに曲がるカーテンレールがあるからそれで作ってみる」

銀二「それは楽しみだな。それから、必ずボールとスロープ間の最大静止摩擦係数を測るのを忘れんとってな」

草太「分かった。またお願いね」

　銀二叔父さんは、数日後にまた仕事で東京にくるというので、そのときに課題を見てもらうことにしました。次の日早速、草太は材料を買いに行き、いよいよ、ピタゴラスイッチの製作に取り掛かりました。まずはスロープからです。

草太のスロープ

図2.9　草太の設計したスロープ

草太「スロープを作ってみた（図2.9）」

銀二「どうだった」

草太「パチンコ玉やビー玉ではダメだったけど、新しいスーパーボールならスロープをうまく乗り越えたよ。スーパーボールでも、つるつるしたのは乗り越えられなかったんだ」

銀二「なるほど。金属ボールではダメだね。ところで、それぞれの摩擦係数は測ったかい？　最大静止摩擦係数の簡単な測定方法は分かっているね」

草太

「斜面を滑り落ちるときの最大傾斜角度をθとしてμ＝tanθ。金属の球が1／6＝0.17で、スーパーボールが3.2／6. 5＝0.49だった。ビデオに実験の様子を撮っておいたから確認してみてよ（図2.10、動画）」

図2.10　ボールが滑るときの傾斜角

草太の撮ったビデオ

金属摩擦係数

スーパーボール摩擦係数

金属玉スロープ

スーパーボールスロープ

銀二「なるほど」

草太「これで摩擦係数が0.4より小さい（図2.7参照）パチンコ玉はスロープを登れないことが、理論からも実験からもはっきりしたね。ピタゴラスイッチを思い付きで作るのも楽しいかもしれないけれど、科学的根拠を考えながら作るのは、わくわくするね」

銀二「そうか、それはよかった。今日は、これから仕事なんだ。すまんが、もう帰るよ。次に会うときまでの宿題を出しておこう。これができたら、次のサブ・システム2のゲートの設計をしようじゃないか」

草太「仕事頑張ってね」

銀二叔父さんから2つの宿題

　銀二叔父さんは、以下のような宿題を2つ置いていきました。以下の表1を参照し、問題を解いてみましょう。

表1　図2.9のスロープの形状データ

問題1

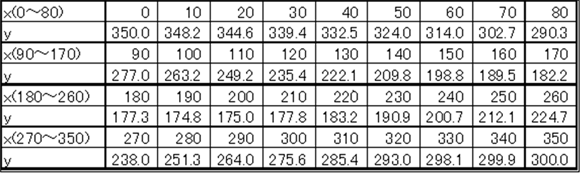
　 図2.9の草太が設計したスロープで、ボールはスロープ全域で接触するものとして、ボールとスロープ間の最大静止摩擦係数は0.6、転がり摩擦係数は全域一定値で0.05、動摩擦係数は最大静止摩擦係数と同じ値であるとして、摩擦によるエネルギー損失を位置エネルギーに換算して計算せよ。またスロープ形状による遠心力は無視すること。

問題2

　最大静止摩擦係数を0.3、転がり摩擦係数0.05としたとき、動摩擦係数は最大静止摩擦係数と同じ値であるとして、摩擦によるエネルギー損失を位置エネルギーに換算して計算せよ。

回答は、4ページ目にあります。

　宿題を解いたら、張り切って次回にのぞみましょう！（次回に続く）

Profile

岩淵正幸（いわぶち まさゆき）

1953年生。技術士（機械部門）。日本セメント（現太平洋セメント）、川崎重工業精機事業部（現カワサキプレシジョンマシナリ）を経て、現在事務処理機器メーカーでシミュレーションを活用した設計方法の開発および設計コンサルティング業務を担当。川崎重工では、油圧制御システム設計、旧石油公団（現石油天然ガス・金属鉱物資源機構）委託研究による圧力波通信システムの開発研究、対戦車用ミサイル操舵装置の開発に従事。

*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***