摩擦係数というより摩擦係数の変数だ：ピタゴラスイッチの計算書を作ろう（2）（2/4 ページ）

摩擦係数μは、斜面を滑りながら転がっているか、または滑らずに転がっているかにより意味が異なるって理解していた？

[岩淵 正幸／技術士（機械部門），＠IT MONOist]

摩擦係数の意味

　草太は（2-11）の摩擦係数μについて、ちょっと誤解しているようです。

　通常、摩擦係数といえば動摩擦係数と最大静止摩擦係数のことを指していますが……。

銀二「ここで使っている摩擦係数μは、もしボールが斜面を滑りながら転がっている場合ならば動摩擦係数を意味しているし、滑らずに転がっている場合ならば最大静止摩擦係数より小さい値を意味しているんだ。

　つまり、

（2-11）のμは、“摩擦係数の変数”なんだ。

　そういう意味では“摩擦係数変数”なんて、呼んだ方がいいかもしれないな」

図2.2　平板上に置かれた物体

草太「滑らずに転がっている場合ならば最大静止摩擦係数より小さい値を意味してる？ 摩擦係数の変数？ どういうこと？」

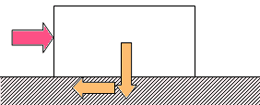
銀二「例えば、図2.2の平板の上に置かれた物体の運動方程式は以下のように書ける」

　もし水平外力Ｑが0ならば物体は当然動きません。

　このとき摩擦係数μは0でなければなりません。μが0でなかったら、右辺は負の値を取るので、物体は負の方向に動き出してしまうのです。

　外力が作用していなければμは0でなければなりません。しかし、わずかでも水平外力が作用すると、μは0ではないのです。

銀二「では、そのときμは最大静止摩擦係数値μ_maxを取るかといえば、そうではない。物体が動かないのだからμはQ とμ・mgが釣り合う値となっている。もし、動く寸前であれば最大静止摩擦係数だし、動いているのであれば動摩擦係数となっている、ということだ。つまり、物体の状態によって、いろいろな値を取る。その意味で変数ということだよ」

草太「Q を徐々に大きくしてやって、最大静止摩擦係数μ_maxとmgとの積の値を超えたとき、（2-12）の右辺が正となって加速度が発生し、初めて物体が動き出すということだね」

銀二「そういうことだね。だから、ボールが滑らずに、スロープを転がる条件は、正確には、こういうことになる」

銀二「上記のことから、どういうことが分かる？」

草太「パチンコ玉のような、最大静止摩擦係数が小さい場合には、例えばμmax＝0.1の場合には、tanθ＝3.5×0.1＝0.35を満足するθは19.3度。

　だから、

　　　　傾斜が19.3度以上の坂ではパチンコ玉は滑りながら転がる

ということになるね」

　逆に、スロープの最大傾斜角を45度とするとボールが滑らないためには最大静止摩擦係数は……、

　　tan（45度）／3.5＝1／3.5＝約0.3

　　⇒　つまり、0.3以上あればいい

ということになります。

　傾斜が大きいほど滑りやすいので、最大静止摩擦係数の大きい材料のボールを選ぶ必要があるということです。

草太「摩擦係数の大きいゴムのボールがいいってことになるかな。でも、エネルギー損失から考えると、摩擦係数が小さければ、いくら滑ったとしてもエネルギー損失が小さいから段差H_sも小さくできるんじゃないの？」

　ですから、

1. 摩擦係数の小さいパチンコ玉にして滑りながら移動させるか？
2. それとも摩擦係数の大きいゴムボールにして転がりながら移動させるべきか？

　が問題ということになりますね。

転がり摩擦

銀二「よく考えてごらん。エネルギー損失はなぜ発生するんだい？」

草太「滑りによる摩擦損失だよ。……あっ、そうか。滑らずに転がればエネルギーは損失しないんだ。だからゴムボールを使うべきなんだ。ボールの選定がポイントって前回いっていたけど、そういうことだったわけか」

図2.3　転がり摩擦：硬いボールが通過する際、この部分を潰すためのエネルギーはボールの力学的エネルギーから提供される。それが転がり摩擦に対応する

　転がっていればエネルギーはまったく損失しないかといえば、そうではありません。

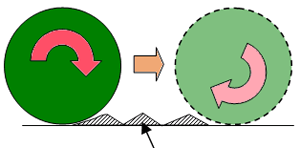
　物体の表面には目では判別できないほど小さな凹凸があります（図2.3）。

　ある物体がほかの物体に接触しながら運動するとき、硬いものが柔らかいものを変形させたり削ったりしているのです。

銀二「その変形や削りに費やされる仕事がエネルギー損失なわけだ。ゴムのような弾性体であっても変形・復元するときには、ゴムの持つ粘性によってエネルギーは失われるんだ。ただ、その損失量は滑る場合に比べて非常に小さいんだ」

草太「じゃあ、転がり摩擦の係数が分かれば、段差H_sはエネルギーの式から計算できるわけだ」

銀二「そういうことになるね。ただし注意する必要があるよ。平地の場合には(2-13)式から摩擦係数は非常に小さくても転がるけど、傾斜が変化するスロープの場合には、傾斜θの大きいところでは(2-13)が満足されなくなる場合が出てくる。そうなると滑りが発生する可能性がある」

　滑りによって大きなエネルギー損失が発生します。

　全域にわたって、滑りが発生しないことが保証されているならば、転がり損失から必要な段差Hsを推定してもよいですが、そうでない場合は、滑りが発生する部分の損失をきちんと見積もる必要があります。

図2.4　正弦波スロープ

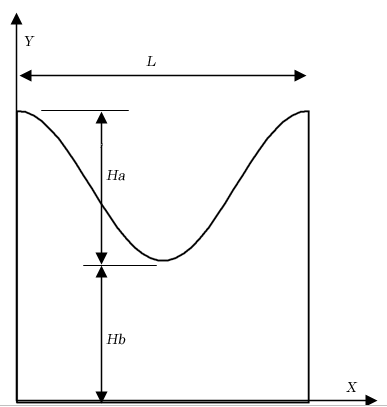
　例えば、図2.4のような正弦波状のスロープの上をボールが移動する場合について考えると、形状は以下のように表せます。

銀二「スロープの傾斜θのタンジェントは、その微分係数だ」

銀二「(2-15)は傾斜の正負を考慮していることに注意しよう。つまり降りの傾斜は負で登りの傾斜が正だということだ。しかし、滑る滑らないの判定に傾斜の正負は関係ないから絶対値を計算して、以下の式を満足する。x ではボールは滑らないということになる」

草太「僕の卒業設計課題では

　　　　L＝350 mm、H_a＝350-170＝180 mm

　だから、（2-16）から、こういう式になるね」

　ボールが滑らずにスロープを転がる、つまり、スロープの全域で最大静止摩擦係数μ_maxが0.46以上となるようなスロープとボールを選定すれば、ボールは全行程を滑らずに動くということになります。

草太「じゃー、やっぱりゴムボールじゃなければダメなんだね。でも最大静止摩擦係数が0.4のボールしか手に入らなければ（2-17）から、滑る領域と転がる領域に分けて、全損失エネルギーを計算してHsを求めることになるんだね。なんか面倒くさいけど、これをしないと、いい設計はできないんだよね」