そこにデータムを付けるのか、付けないのか：製図を極める！ 幾何公差徹底攻略（6）（2/2 ページ）

今回は製図の際に多くの設計者が戸惑う悩みの1つ「データムを付けるのか付けないのか」をスッキリ解決する。

[山田学 ラブノーツ／六自由度技術士事務所，MONOist]

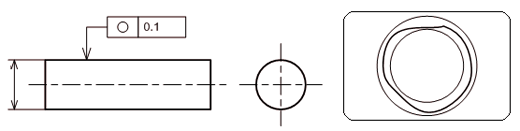
真円度

　JISによると、「真円度（Roundness）とは、円形形体の幾何学的に正しい円からの狂いの大きさをいう」と定義されます。まん丸であって欲しいという形体に対して指示するものです。

　通常円筒は旋盤加工されるため、円形が大きく崩れることはありません。一般的な産業機械での使用頻度は低いと思われますが、エンドミルの工具そのもののように機能上、真円からの崩れが許されない場合に用います。

　図3に示す図面例は、幾何公差の矢の当てた面に対して任意の位置で直角方向に輪切りした切り口の稜線が0.1mmの幅を持った2円間の中にあれば合格品と判断されるものです。丸軸における母線が対象部位ですので、幾何公差値にφは付きません。

図3　真円度の指示例と領域

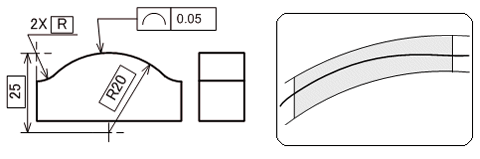
線の輪郭度

　JISによると、「線の輪郭度（Profile of a line）とは、理論的に正確な寸法によって定められた幾何学的輪郭からの線の輪郭の狂いの大きさをいう」と定義されます。

　意匠面（デザイン面）など局面などを持つ形体に対して、データ通りの形状であって欲しいという場合に指示するものです。

　通常意匠面は、複雑あるいは微妙な曲線などが組み合わさり設計されるため、座標測定器を用いて3次元データと比較して計測されます。

　図4に示す図面例は、幾何公差の矢の当てた面に対して任意の位置で平行方向（図面奥行き方向）に輪切りした切り口の稜線が0.05mmの幅を持った指定された曲線間の中にあれば合格品と判断されるものです。曲面を構成する線要素が対象部位ですので、幾何公差値にφは付きません。

図4　線の輪郭度の指示例と領域

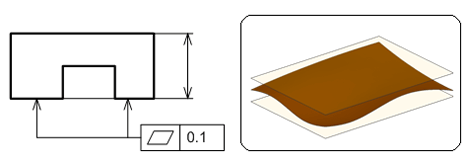
平面度

　JISによると、「平面度（Flatness）とは、平面形体の幾何学的に正しい平面からの狂いの大きさをいう」と定義されます。

　まっ平らであって欲しいという形体に対して指示するものです。通常円平面はフライス盤加工されるため、平面が大きく崩れることはありません。一般的な産業機械での使用頻度は低いと思われますが、特に平面部の面積が多い場合など、加工熱によって反りが発生する可能性が高くなります。機能上、反りが許されない場合に用います。

　図5に示す図面例は、幾何公差の矢の当てた面に対して、左右の面それぞれが単独の面として0.1mmの幅を持った平行2平面間の中にあれば合格品と判断されるものです。平らな表面が対象部位ですので、幾何公差値にφは付きません。

図5　平面度の指示例と領域：右側の領域を表すイラストは1つの平面で表していますが、左右独立して平面度を評価します。左右同時に評価する場合は、図6を参照ください

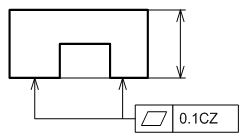
　離れた形体を同時に平行2平面間の幅の中で規制したい場合は、公差値の後ろに「CZ」を追記します。CZとは、共通領域（Common Zone）の意味です。複数の面が同一面上に取り付く場合、CZ表記が必要です。

図6　CZ表記

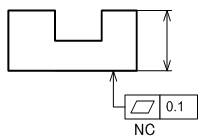
　平面の反り方向を規制したい場合は、公差記入枠の下に「NC」を追記します。NCとは、中高でない（Not Convex）の意味です（図7）。

図7　NC表記

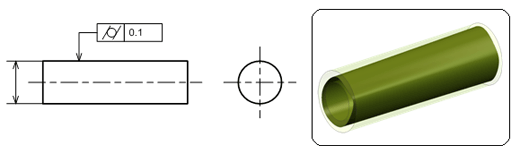
円筒度

　JISによると、「円筒度（Cylindricity）とは、円筒形体の幾何学的に正しい円筒からの狂いの大きさをいう」と定義されます。

　まん丸かつ真っすぐであってほしいという形体に対して指示するものです。通常円筒は旋盤加工されるため、円形が大きく崩れた状態で反りが発生することはありません。一般的な産業機械での使用頻度は低いと思われますが、機能上、曲がりのない真円を持つ円筒形状からの崩れが許されない場合に用います。

　図8に示す図面例は、幾何公差の矢の当てた面全体にわたり0.1mmの幅を持った曲がりのいない2円筒間の中にあれば合格品と判断されるものです。丸軸における母線が対象部位ですので、幾何公差値にφは付きません。

図8　円筒度の指示例と領域

　一般的に検査が大変であることから3次元測定機が必要となります。従って、積極的に使用はお勧めしません。

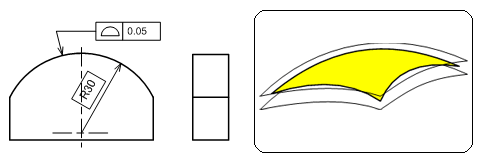
面の輪郭度

　JISによると、「面の輪郭度（Profile of a surface）とは、理論的に正確な寸法によって定められた幾何学的輪郭からの面の輪郭の狂いの大きさをいう」と定義されます。

　意匠面（デザイン面）など局面などを持つ形体に対して、データ通りの形状であって欲しいという場合に指示するものです。

　通常意匠面は、複雑あるいは微妙な曲線などが組み合わさり設計されるため、座標測定器を用いて3次元データと比較して計測されます。

　図9に示す図面例は、幾何公差の矢の当てた面全体にわたり0.05mmの幅を持った指定された曲線間の中にあれば合格品と判断されるものです。曲面が対象部位ですので、幾何公差値にφは付きません。

図9　面の輪郭度の指示例と領域

　今回は6種類の形状公差について確認しましたが、設計上で必要な幾何特性を判断できるように、その理解を十分に深めてください。

---

　次回以降に解説する幾何特性（姿勢公差、位置公差、振れ公差）は形状公差と違い、全て相対比較するための基準、つまりデータムを必要とします。

　次回は4つに分類される幾何特性のうち角度を制御する姿勢公差です。平行や直角という角度を規制するものですから、大変理解しやすく利用頻度も多く設計者として利用しやすい特性です。（次回に続く）

◎併せて読みたい「CAD」関連ホワイトペーパー：

» 主要7製品を完全網羅！　製品選定・比較に役立つ「商用3D CADカタログ 完全版」

» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”

» 設計現場の56.5％が3D CADを活用、2次元からの「移行予定なし」も16.7％

» エクスペリエンス時代に向けて進化を続ける「CATIA」

» PTCが語る3D CADの歴史と「Creo」の注目機能

⇒ CAD関連の新着ホワイトペーパーはこちら

Profile

山田 学（やまだ まなぶ）

1963年生まれ。ラブノーツ代表取締役、技術士（機械部門）。カヤバ工業（現、KYB）自動車技術研究所で電動パワーステアリングの研究開発、グローリー工業（現、グローリー）設計部で銀行向け紙幣処理機の設計などに従事。兵庫県技能検定委員として技能検定（機械プラント製図）の検定試験運営、指導、採点にも携わる。2006年4月、技術者教育専門の六自由度技術士事務所を設立。2007年1月、ラブノーツを設立し、会社法人（株式会社）として技術者教育を行っている。著書に『図面って、どない描くねん！』『読んで調べる 設計製図リストブック』（共に日刊工業新聞社刊）など。