ピンポン球を使って6自由度について説明してみた:設計者CAEを始める前にシッカリ学ぶ有限要素法(4)(1/3 ページ)
ピンポン球が1個、箱の中にあって、天井からひもでぶら下がっている。実はこのピンポン球が有限要素の“何か”。
前回は、有限要素法の主役である三大要素について説明しました。有限要素法は、その名が示すとおり、「要素」が主役です。もう少しだけ要素について解説させてください。
要素のことなど、細かく知らずとも解析はできます。何らかの結果も得られるでしょう。それでも要素について知っていていただきたいのは、有限要素法の解析では結局のところ、要素が解析結果の精度を左右するからなのです。有限要素であるがゆえの特性もあって、それが解析結果をときに大きく変えてしまうことすらあります。つまり要素についてシッカリと知っていれば、その特性やクセの向こう側にある解析結果の本質に迫ることができるというわけです。退屈な話が続くと思いますが、どうぞお付き合いくださいね。
1.ピンポン球の自由な振る舞いを測るには
節点には「自由度」があります。自由度とは読んで字のごとし。その節点が動く可能性がある方向を成分で表したものです。節点は、有限要素を説明するうえで必要な概念です。そして自由度は、節点を説明するうえで必要な概念です。まずは自由度について説明していきます。
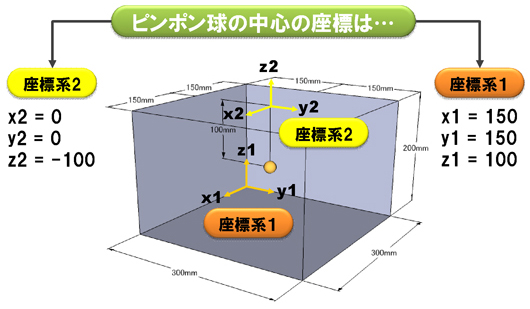
ここでピンポン球が1個、縦、横、高さがそれぞれ、300mm、300mm、200mmの箱の中にあり、天井からヒモでぶら下がっているとイメージしてみましょう。ヒモの長さは、高さのちょうど半分の100mmです。
さて、そのピンポン球はどんなふうに動くのでしょうか。それを「定量的に」説明するために、「座標系」という概念を取り入れてみましょう。
座標系とは、「空間の任意の点を定量的に表すための基準」のことです。座標系の取り方は自由です。例えば、箱のスミを原点にした座標系1(x1,y1,z1)では、ピンポン球の中心は以下のように表されます。
(x1,y1,z1) =(150,150,100) (単位:mm)
次にピンポン球がぶら下がっているヒモの天井側の端点を原点とする座標系2(x2,y2,z2)を考えてみましょう。ピンポン球の中心は以下のように表されます。
(x2,y2,z2) =(0,0,-100) (単位:mm)
数字で表される座標値は全然違いますが、座標系が違うため、3次元空間の中では、まったく同じ位置を表しています。
栗サンの「一休みコラム」栗サンの「一休みコラム」:緯度、経度って何だろう?
今回使用したような、3つの軸が直交している座標系を「直交座標系」といいます。空間上の任意の1点はすべてこの直交座標系で表すことができます。でも円筒や球だと、直交座標系を使った場合、とっても面倒になる場合があります。そういう場合は、直交座標系意外の座標系を定義するワケです。例えば、地球上でアナタのいる、そう、その位置。その座標ってどうやって表しますか? そう、答えは「緯度・経度」です! カーナビはこの緯度と経度を人工衛星から算出して、アナタの車の位置を特定しているのです。緯度と経度について、ここで僕がクドクドと説明するよりも、イラスト付きで楽しく説明してくれているホームページがあるので、それを紹介しておきます。
このホームページを読んで、ちょっとビックリしたのですが、2001年から緯度と経度が変わったのですね。距離にして400m強、ズレたってわけです。知らなかったです。
さて、話を「箱の中につるしたピンポン球」に戻しましょう。このピンポン球、どっち方向に動きますか?
感覚的に「あっちだ、こっちだ」といっていても、よく分からないので、定量的に話を進めるために、ピンポン球の中心部に、直交座標系を設定してみます。これで、ピンポン球が動く方向を、定量的に表すことができます。
これでピンポン球が揺れてどんな位置に来ても、ピンポン球の位置を表すことができるようになります。ピンポン球のヒモが切れて、箱の中のどこかに転がっても、それは同じこと。さらに、ピンポン球が箱を飛び出しても、ピンポン球の位置は特定できます。
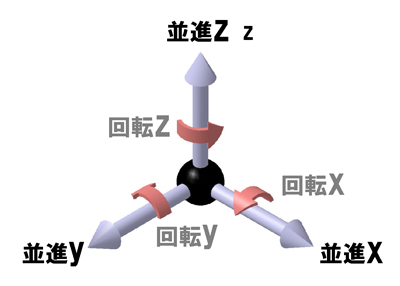
ピンポン球は、回転せずにスライドするだけの場合もあります。このスライドを「並進」と呼び、x,y,zで表されます。また当然のことながら、ピンポン球は回転します。その回転はx,y,zに対応し、それぞれθx,θy,θzで表されます。
ピンポン球がヒモに吊るされている場合、並進xのプラス、マイナス両方向、並進yのプラス、マイナス両方向、そして並進zはプラス方向のみで、ピンポン球の移動を表すことができます。並進zにマイナス方向がないのは、ピンポン球にはヒモが付いているため、「ヒモの長さ以上に下に行かない」ということです。
ピンポン球のヒモが切れてどこにいっても、その位置は並進のx,y,zと回転のθx,θy,θzで表されます。ピンポン球の動きの自由な度合いを示すこと、それが、自由度です。並進3成分、回転3成分、合わせて6成分。これを「6自由度」と呼びます。
栗サンの「一休みコラム」:6自由度といえば……
6自由度というのは、このサイトの読者さんにはなじみのある言葉ではないでしょうか。「演習系山田式 機械製図のウソ・ホント」をお書きになっている山田学さんの会社名が、そう、「六自由度」なのです。この会社名を初めて知ったとき、思わず、ニヤリとしてしまいました。山田さんの著書には、面白いタイトルが並びます。「図面って、どない描くねん!」は、図面の描き方の「いろは」を教えてくれます。そういう意味で、僕の「材料力学」と視点が似ているので、六自由度の社名とともに、とても親近感を持っています。
これまでの本連載の記事でお分かりいただけたと思いますが、解析しようとしている部品は、節点と要素のカタマリなのです。そして「部品に荷重が掛かって変形する」ということは、「節点が動く」ということなのです。節点が動くということは、その節点の移動を定量的に測らなければならない、ということです。定量的に測るということは、そこに座標系が必要なのです。そして座標系は6つの方向に動く可能性があるということを示唆しています。
先ほどのピンポン球を節点に置き換えてみてください。ピンポン球は節点そのものなのです。このセクションの締めくくりとして、次のことを覚えておいてください。
Copyright © ITmedia, Inc. All Rights Reserved.