設計で欠かせない「ミーゼス応力」を押さえよう:仕事にちゃんと役立つ材料力学(4)(2/3 ページ)
ミーゼス応力は設計にとって非常に大切な応力だ。材料の持つ固有の値と比較することでその材料を使った部品の強度を判定できる。
応力のいろいろ
これまでの解説で、「応力=単位面積当たりの力」だということや、その単位も理解できたと思います。さて、ここからは部品に対してどういうふうに応力が作用するのか、片持ちばりを例に挙げて解説していきます。
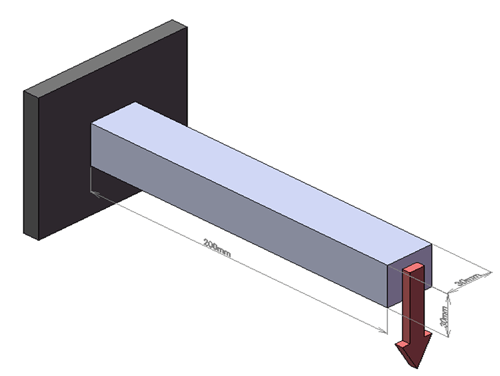
まず、断面が30mm×30mmの長さ200mmの片持ちばりをイメージしてみましょう(図1)。
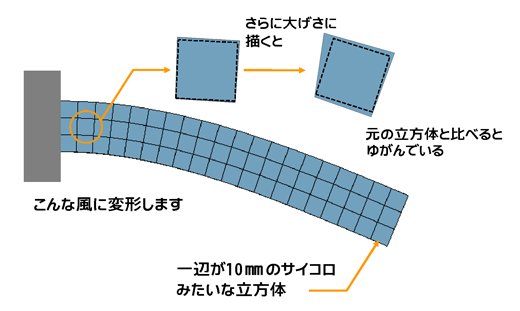
そして、片持ちばりの先端に荷重を掛け、はりが変形した様子をイメージしてください。さらに、この片持ちばりの表面に10mmピッチで線を引きます。
ピッタリと線が引けますね? グイッと変形した状態でこの10mmの格子状の線をよく観察すると、以下のようなことが分かります。
- 荷重を掛けた先端は格子が正方形のままで、ほとんど崩れていないぞ?
- 固定した部分の正方形は、かなりゆがんでいるぞ?
- 荷重を掛けた端から、固定した端に近づくにつれて、正方形のゆがみがひどくなっているぞ?
などです。
この10mmピッチの線に沿って、豆腐をサイの目状に“アタマの中で”切ってください。そして固定端に近い部分の1つを“アタマの中で”引っこ抜いて、手のひらの上に乗っけてみてください。ゆがんだサイコロのようなものがアナタの手のひらには乗っかっているはずです(図2)。
なぜ、この立方体はゆがんでいるのか? それは荷重によって変形が起こり、ゆがみ、そして、応力が発生しているのです。
ここでは片持ちばりで10mm角のサイコロを切り出して考えてみました。それでは片持ちばりを皆さんの設計している部品に置き換えて、10mm角のサイコロを極限に小さいサイコロで考えてみましょう。
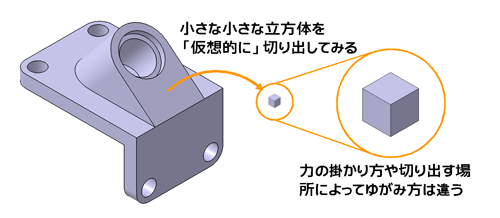
「“極限に小さい”って、いったいどれくらい小さいの?」と質問がきそうなので、ここでは1mm角ということにしておきましょう。アナタの設計している部品に力が掛かり、その小さな1mm角のサイコロが変形し、応力が発生します(図3)。
その小さなサイコロは、力の掛かり方によって、あるいは部品のどの部分かによって、さまざまな形にゆがみます。
どんなゆがみでも、そのゆがみを表す応力は、仮想的に切り出したサイコロの面に垂直な成分と、面に平行な成分に分解できます。
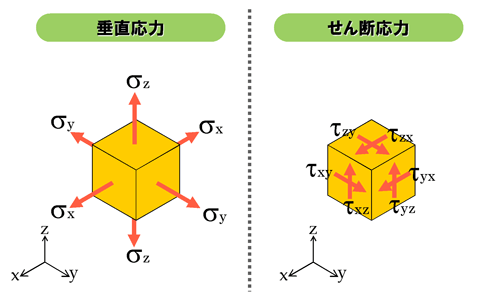
- 面に垂直な応力の成分を「垂直応力」といって、一般的にはσ(シグマ)で表します。
- 面に平行な応力の成分を「せん断応力」といって、一般的にはτ(タウ)で表します。
「せん断」という言葉の意味については、次のページで説明します。ここでは取りあえず、「そういう言葉なんだ〜」ぐらいに理解しておきましょう。
アタマの中で仮想的に切り出したサイコロ立方体には、6面全部にこれらの応力が発生しています。サイコロの各辺に平行な直交座標系(x,y,z)を設定し、それを使って方向を表現しています(図4)。
。oO 筆者のつぶやき
どうして材力ってギリシャ文字だらけなのかな?
ギリシャ文字を使った途端、何だか妙に難しく見えてしまうのは僕だけでしょうか。材料力学の教科書では、ギリシャ文字は日常茶飯事に使われます。「なんでわざわざギリシャ文字を使わなきゃならないのだろう? 英語のアルファベットでも構わないのになぁ」と、ずっと思っていましたし、いまでもそう思ってます。
ひとまず、応力についてのまとめ
ここまでの応力についての解説をまとめます。
- 構造物に荷重が掛かると、応力が発生します。
- 応力は単位面積当たりの力です。
- 応力には、垂直応力とせん断応力という成分があります。
応力について長々と説明してきましたが、この時点では、上記3つのポイントが理解できていればOKです。
Copyright © ITmedia, Inc. All Rights Reserved.